A given mass of oxygen at room temperature occupies a volume of 500.0 mL at 1.50 atm pressure. What pressure must be applied to compress the gas to a volume of only 150.0 mL?
1 Answer
Explanation:
The idea here is that pressure and volume have an inverse relationship when temperature and number of moles are kept constant, as described by Boyle's Law.
This implies that decreasing the pressure by a given factor, let's say
Similarly, increasing the pressure by a factor
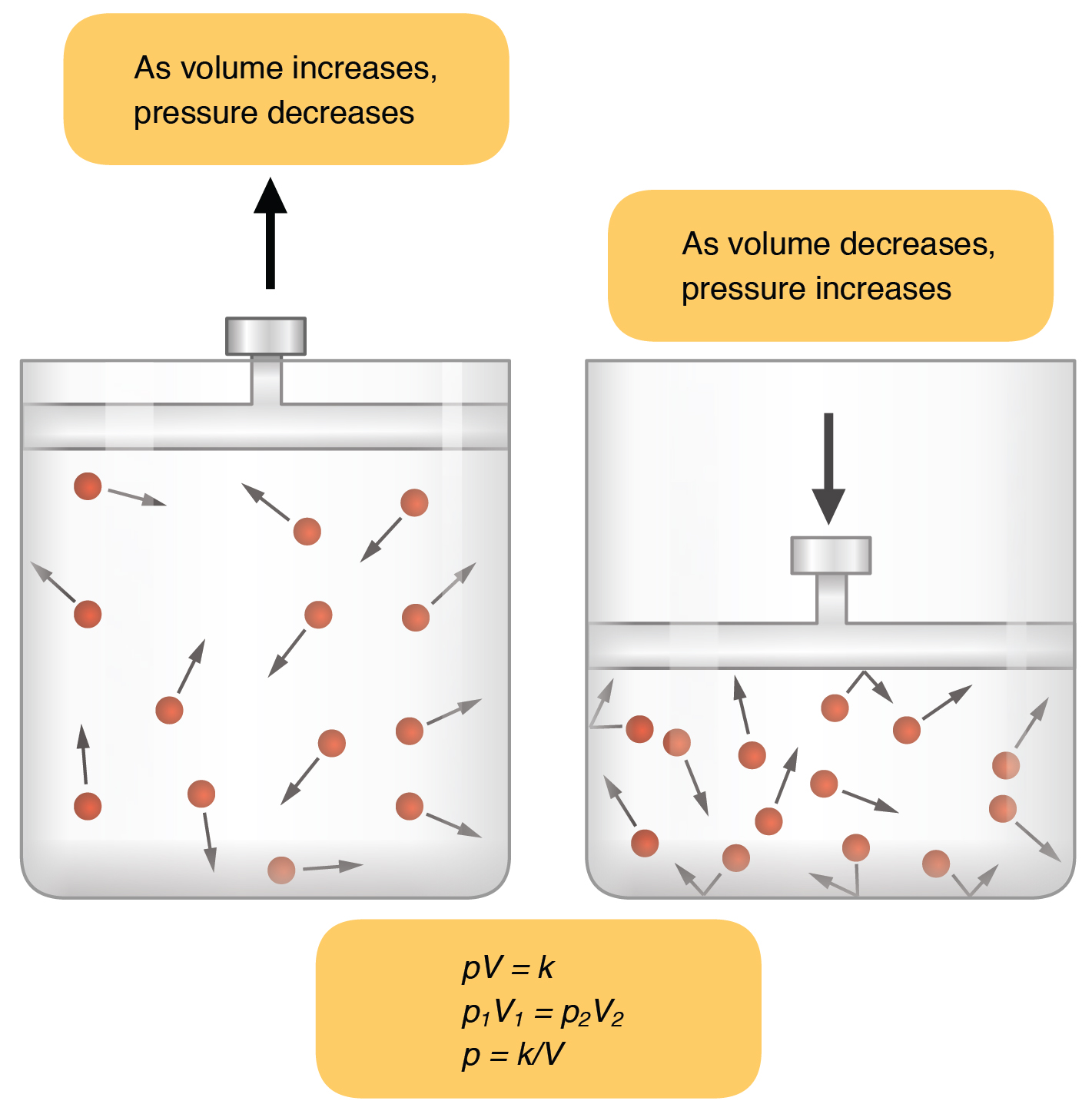
In your case, the volume decreases by a factor of
#(500.0color(red)(cancel(color(black)("mL"))))/(150.0color(red)(cancel(color(black)("mL")))) = color(blue)(10/3)#
This means that the pressure of the gas increased by a factor of
#P_"final" = color(blue)(10/3) * "1.50 atm" = color(green)(|bar(ul(color(white)(a/a)color(black)("5.00 atm")color(white)(a/a)|)))#
The answer is rounded to three sig figs, the number of sig figs you have for the initial pressure of the gas.

