Question

A model train with a mass of `2 kg` is moving along a track at `9 (cm)/s`. If the curvature of the track changes from a radius of `6 cm` to `25 cm`, by how much must the centripetal force applied by the tracks change?

Answer 1

The change in centripetal force is `=0.2052N`

Explanation:

The centripetal force is

`vecF_C=(mv^2)/r*vecr`

The mass is of the train `m=2kg`

The velocity of the train is `v=0.09ms^-1`

The radii of the tracks are

`r_1=0.06m`

and

`r_2=0.25m`

The variation in the centripetal force is

`DeltaF=F_2-F_1`

The centripetal forces are

`||F_1||=2*0.09^2/0.06=0.27N`

`||F_2||=2*0.09^2/0.25=0.0648N`

`DeltaF=F_1-F_2=0.27-0.0648=0.2052N`

Answer 2

`0.378" N"`

Explanation:

Consider a diagram:

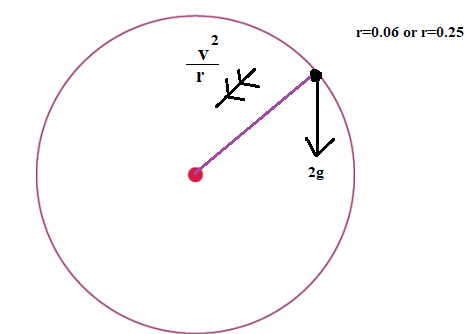
We know that centripetal acceleration, towards the centre, is `a=v^2/r`

`v=9" cm s"^-1`
`=0.09" m s"^-1`

Now, use the formula to find the acceleration in each case for each radius.

Let `a_1` be the acceleration for `6"cm"` and `a_2` be the acceleration for `25"cm"`

`a_1=0.09^2/0.06`
`=0.135" m s"^-2`

`a_2=0.09^2/0.25`
`=0.324" m s"^-2`

Now, since the acceleration will be towards the centre of the circle, resolve forces towards the centre using Newton's Second Law

`F_1=2xx0.135`
`=0.27" N"`

`F_2=2xx0.324`
`=0.648" N"`

So the increase in centripetal force is:

`DeltaF=0.648-0.27`
`=0.378" N"`