A parallelogram has sides with lengths of 14 and 9 . If the parallelogram's area is 63 , what is the length of its longest diagonal?
1 Answer
Explanation:
Consider the parallelogram of the figure below where
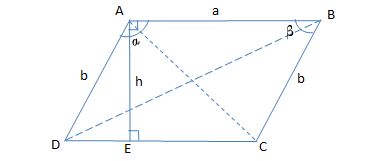 I created this figure using MS Excel
I created this figure using MS Excel
In this figure I made
Comparing the triangles ABC and ABD it's intuitive that the long diagonal is BD because this segment is opposed to an internal angle (
So we want to find BD
In
Finding
Applying the Law of Cosines to
BD^2=a^2+b^2-2abcosalpha
BD^2=a^2+b^2-2a cancel(b)(-sqrt(b^2-h^2)/cancel(b))
BD^2=a^2+b^2+2a*sqrt(b^2-h^2)
And we know that
So
BD^2=14^2+9^2+2*14*sqrt(9^2-(9/2)^2)
BD^2=196+81+28*(9/2)*sqrt(4-1)
BD^2=277+126sqrt(3)
BD=sqrt(277+126sqrt3)~=22.254
By the way, in this question

