Question

A parallelogram has sides with lengths of `15` and `12`. If the parallelogram's area is `120`, what is the length of its longest diagonal?

Answer 1

There is no formula for the area of parallelogram with its diagonals.So, there are no answers for this

Answer 2

`=25.24`

Explanation:

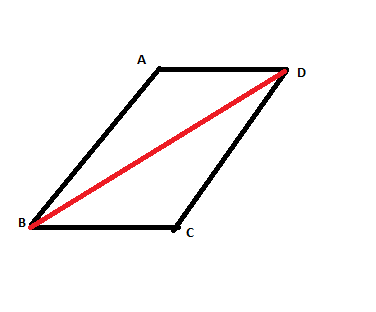
Let in the parallelogram ABCD the angle between two sides `AB=15 and BC= 12` be `/_ABC=theta`
Area of the parallelogram `=AB*BC*sintheta =120 =>15*12sintheta =120=>sintheta=2/3`
`:. theta =sin^-1(2/3)=41.8 deg`
So diagonal BD will be longest which is opposite to obtuse angle `/_BCD`
Now `BD^2=BC^2+CD^2-2BC*CDcos/_BCD`
`=>BD^2=BC^2+CD^2-2BC*CDcos(180-/_ABC)`
`=>BD^2=BC^2+CD^2-2BC*CDcos(180-theta)`
`=>BD^2=BC^2+CD^2+2BC*CDcos(theta)`

`=>BD^2=12^2+15^2+2*12*15*sqrt(1-sin^2theta`
`=>BD^2=12^2+15^2+2*12*15*sqrt(1-(2/3)^2`
`=>BD^2=12^2+15^2+2*12*cancel15^5*sqrt5/cancel3`
`=>BD^2=144+225+268.33`

`=>BD=sqrt(144+225+268.33)=25.24`