Question

A parallelogram has sides with lengths of `15` and `8`. If the parallelogram's area is `12`, what is the length of its longest diagonal?

Answer 1

Length of longest diagonal `22.974` (approx.)

Explanation:

Using a side of length `8` as the base,
since the area is `12`
the height relative to a side of length `8` is `color(purple)(h=12/8=3/2)`

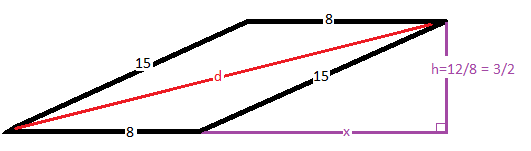
The required diagonal (`color(red)(d)`) is
the hypotenuse of a right triangle formed by extending the base by an amount `color(purple)(x)` until the line segment terminates at a point which is at a right angle under the furthest upper vertex of the parallelogram.

The length of this extension (`color(purple)(x)`) can be calculated using the Pythagorean Theorem:
`color(white)("XXX")color(purple)x=sqrt(15^2-h^2)~~14.928` (using a calculator)

The requested diagonal now can also be calculated using the Pythagorean Theorem as:
`color(white)("XXX")color(red)d=sqrt((8+x)^2+h^2) ~~22.974` (again with a calculator)