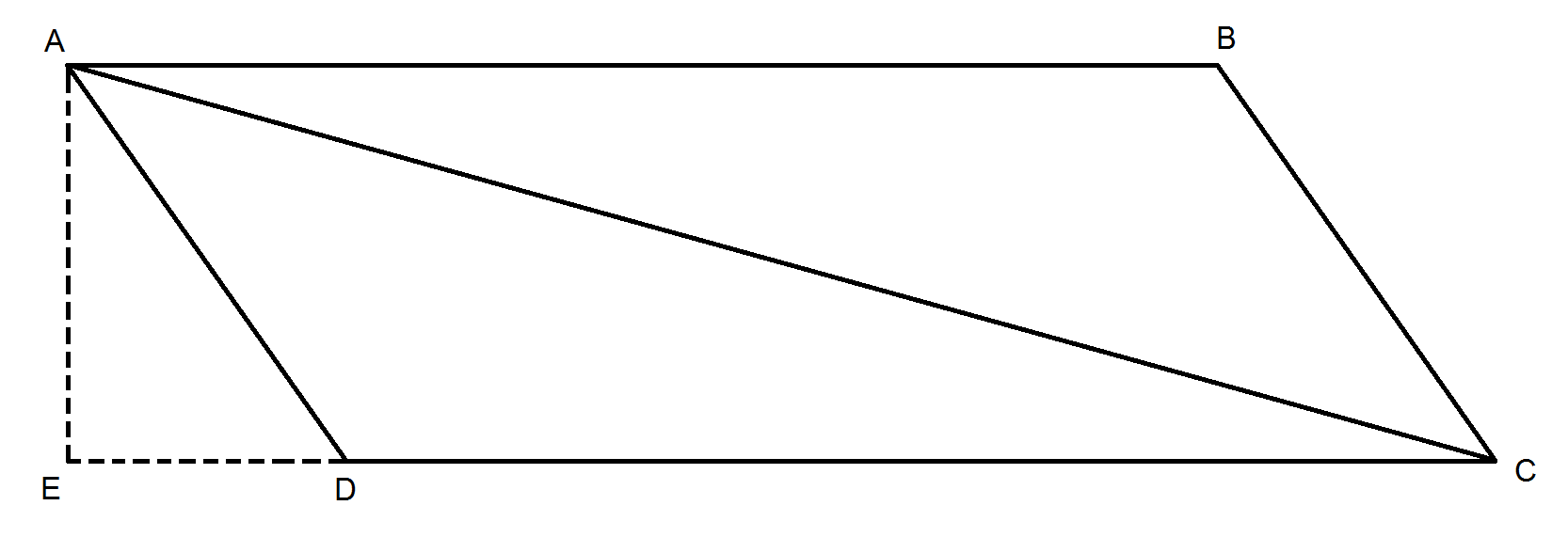
The problem is to find #AC# in the image above, given
#AB=CD=18#
#AD=BC=4#
#"Area"_(ABCD)=48#
As the area of a parallelogram is given by the product of its base and height, we have #AE*CD=48#. Thus
#AE = 48/(CD)=48/18=8/3#
As #triangleAED# is a right triangle, we may apply the Pythagorean theorem to find that #AE^2+ED^2=AD^2#. Substituting in our known values for #AE# and #AD#, we get
#(8/3)^2+ED^2=4^2#
#=> ED=sqrt(16-64/9) = sqrt(80/9)=(4sqrt(5))/3#
As #triangleAEC# is also a right triangle, we can apply the Pythagorean theorem once more to get #AE^2+EC^2=AC^2#. As #EC = ED+CD#, we can once again substitute in our known values:
#AC^2 = AE^2+(ED+CD)^2#
#= (8/3)^2+((4sqrt(5))/3+18)^2#
#=340+48sqrt(5)#
Then, taking the square root, we get our final result:
#AC = sqrt(340+48sqrt(5)) ~~21.15#


