Question

A parallelogram has sides with lengths of `24` and `9`. If the parallelogram's area is `96`, what is the length of its longest diagonal?

Answer 1

Length of the longest diagonal AC is 32.3109

Explanation:

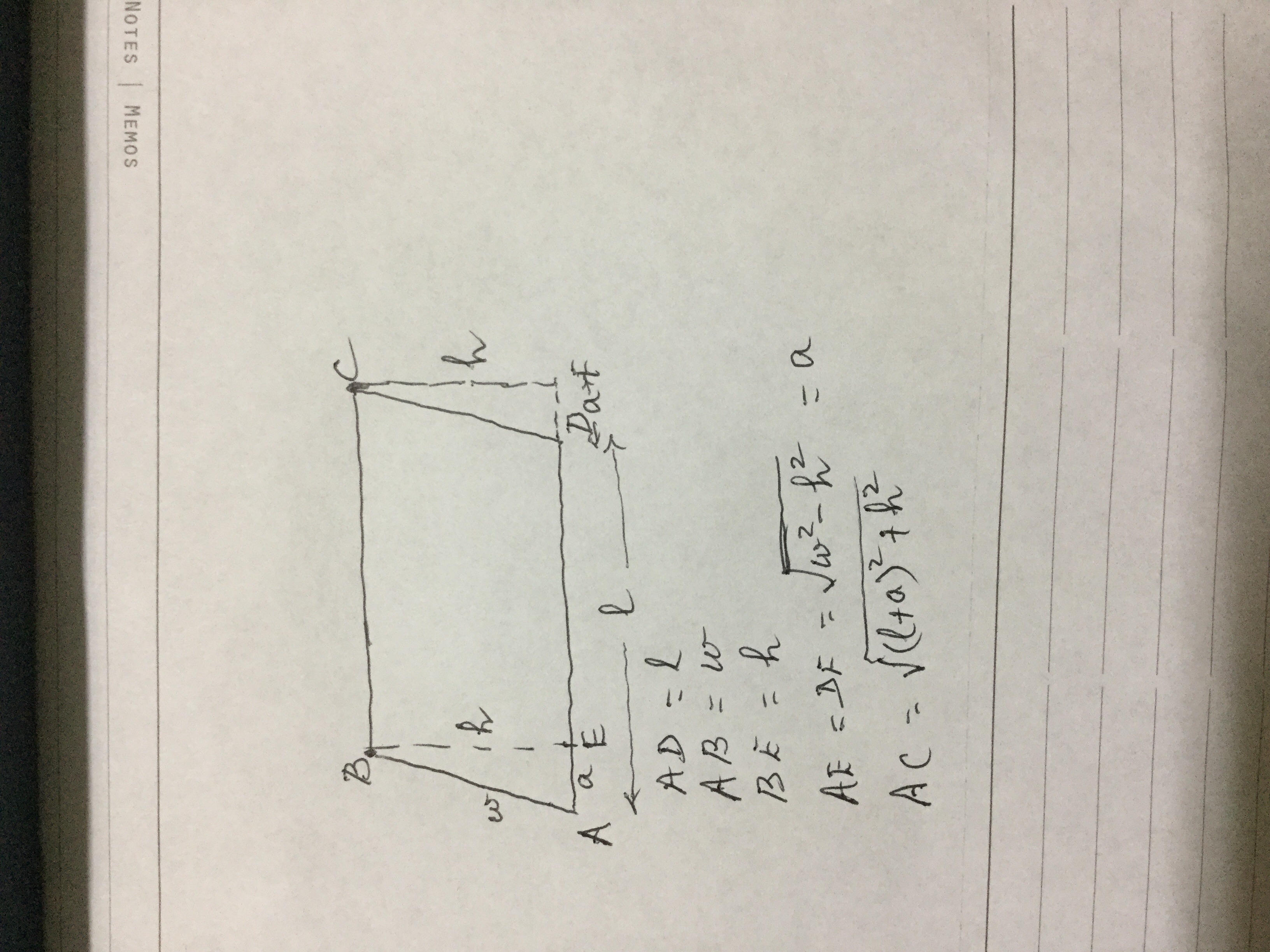
Given `l = 24, w = 9, Area = 96`

Area of the parallelogram = l * h = 96
`:. BE = CF = h = (Area)/l = 96 / 24 = 4`

AE = DF = a = sqrt(w^2-h^2) = sqrt(9^2 - 4^2) = 8.0623#

AF = l + a = 24 + 8.0623 = 32.0623#

Longest diagonal AC #= sqrt(AF^2 + CF^2) = sqrt(32.0623^2 + 4^2) = 32.3109#