A parking lot is to be formed by fencing in a rectangular plot of land except for an entrance 12 m wide. How do you find the dimensions of the lot of greatest area if 300 m of fencing is to be used?
1 Answer
Jan 8, 2016
The maximum area is obtained if the plot is
Explanation:
The perimeter of the plot must be
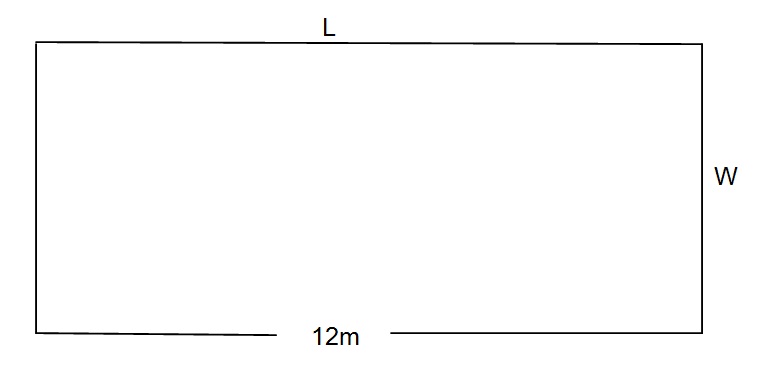
The perimeter is given by
For a quadratic of the form
For this parking lot
So the maximum area of the plot is 6084 sq .m.
Therefore the are of the plot is maximized if the plot is

