A playground, which measures 50m by 35m, is to be doubled in area by adding a strip of uniform width around the outside of the existing area. What is the width of the new strip around the playground?
1 Answer
Explanation:
With problems of this type it becomes much clearer if you do a quick sketch.
The inner area is
The outer strip area is
Combining the outer strip and the inner area doubles the inner area. So our model becomes:
Subtract 3500 from both sides
Simplifying the numbers a bit. 4 will not divide exactly into 1750. However, all the numbers are even so we can at least halve them
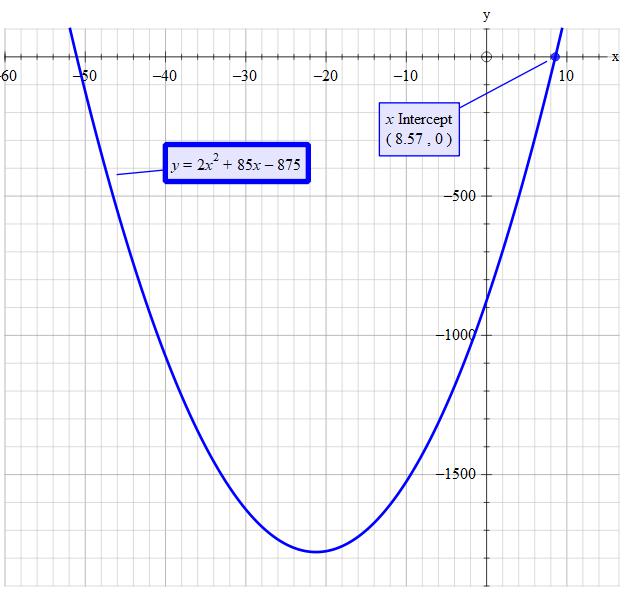
If you can not spot the whole number factors quickly don't waste time in an exam continuing to try and determine them. Use the formula.
The negative final value is not logical so is dismissed.