A point on an island is located 24miles southwest of a dock. A ship leaves the dock at 1:00pm traveling west at 12 miles per hour. At what time(s) to the nearest minute is the ship 20miles from the point?
1 Answer
Explanation:
Warning: This question was asked under "Law of Cosines". The following does not use the "Law of Cosines"
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
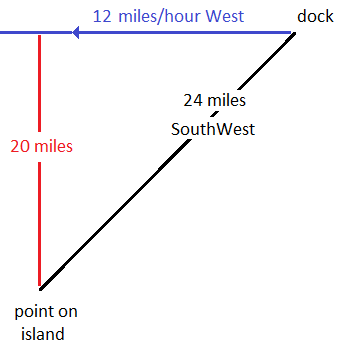
Based on the Pythagorean Theorem
the boat must travel
to be
The ratio of distance to time for the boat is
Traveling
