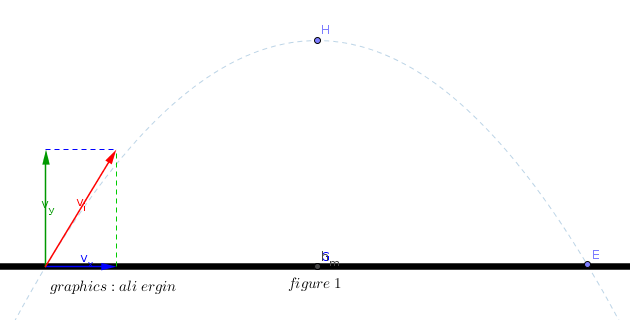
#"The velocity of projectile can be split two components as vertical and horizontal"#
#"the vertical component can be calculated using the formula:"#
#v_y=v_i*sin alpha-g*t" "figure" "1#
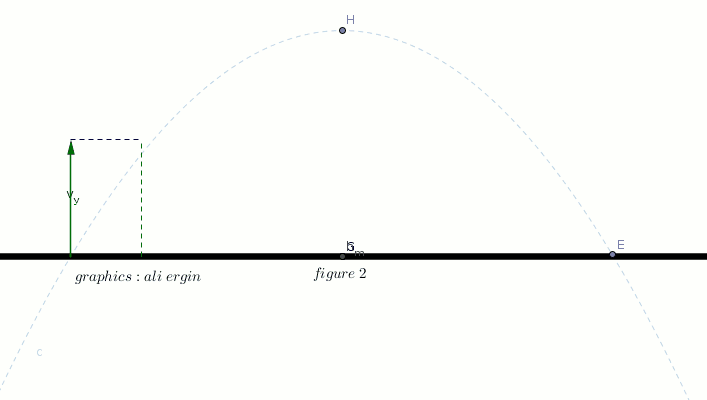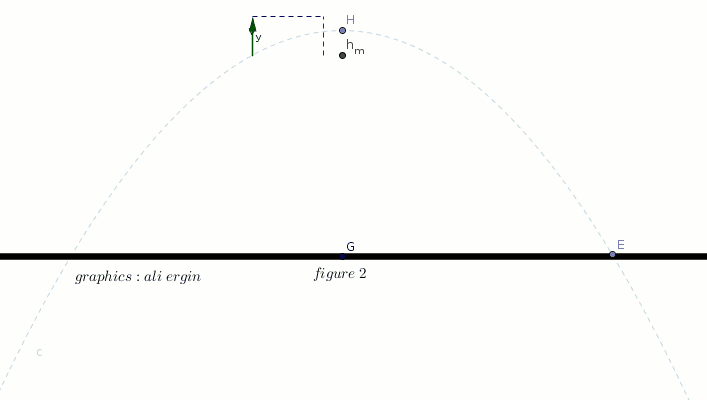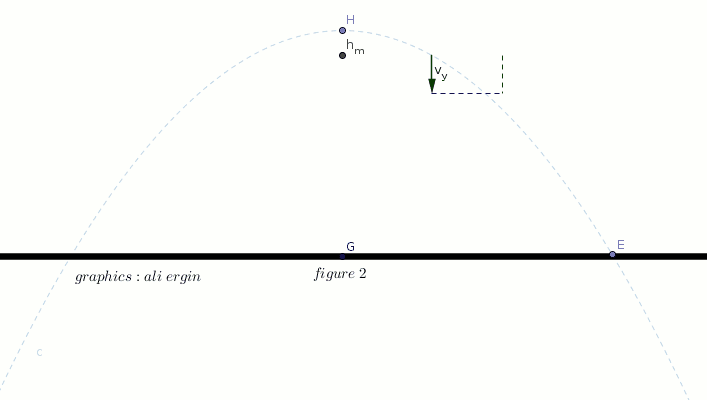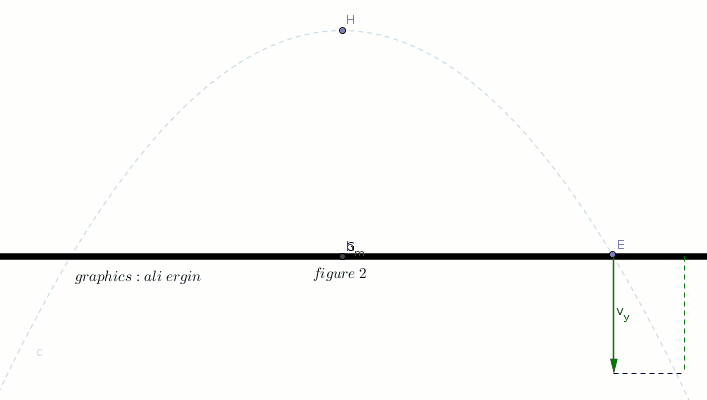
#"you are seeing how the vertical component of velocity is changing "#
#"please note that the vertical component of velocity " v_y" is zero at maximum height"#
#0=v_i*sin alpha-g*t#
#g*t=v_i*sin alpha#
#t=(v_i*sin alpha)/g" time elapsed to the maximum height"#
#"2*t gives us the traveling time"#
#color(red)(t_t=(2*v_i*sin alpha)/g)#
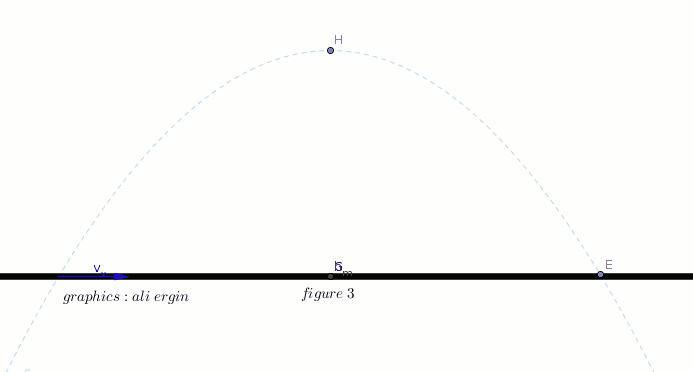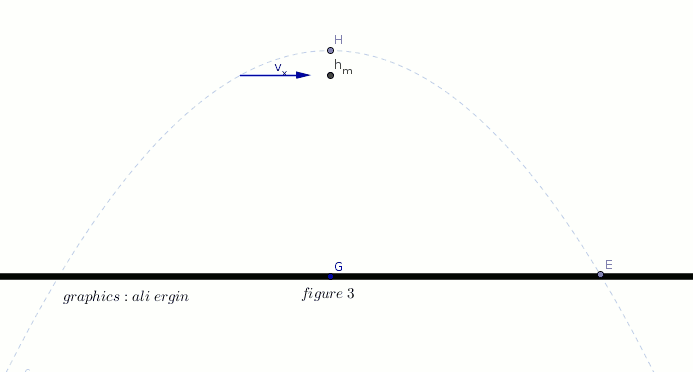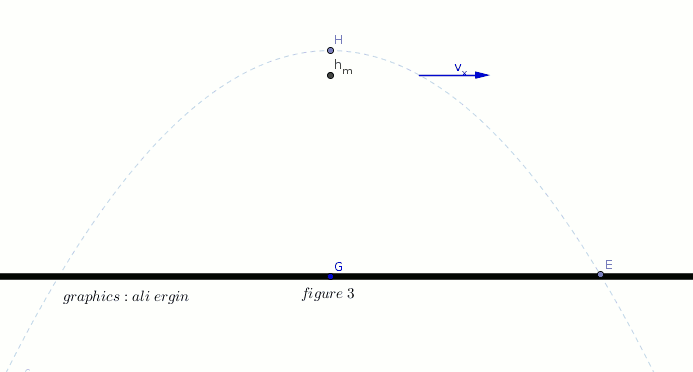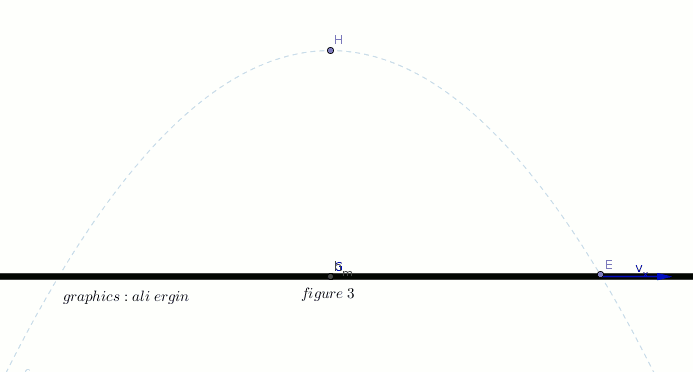
#"the object is conveyed by the horizontal component of velocity "v_x" figure 3"#
#"the horizontal component of velocity is calculated by:"#
#color(green)(v_x=v_i*cos alpha)#
#"the horizontal component of velocity doesn't change"#
#"and doesn't depend on time"#
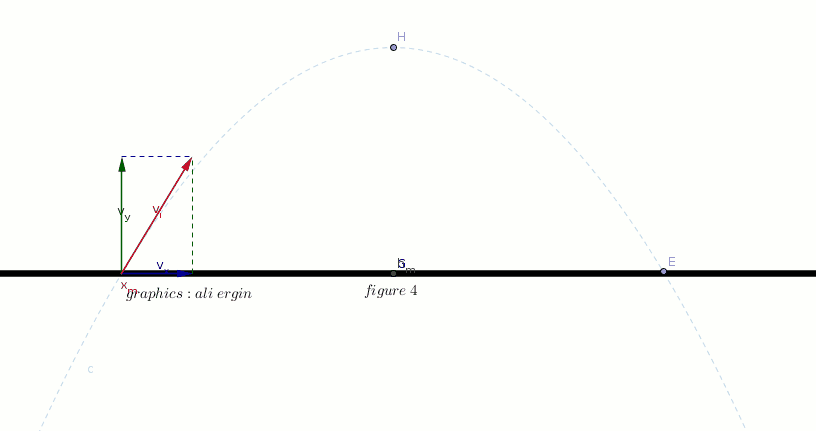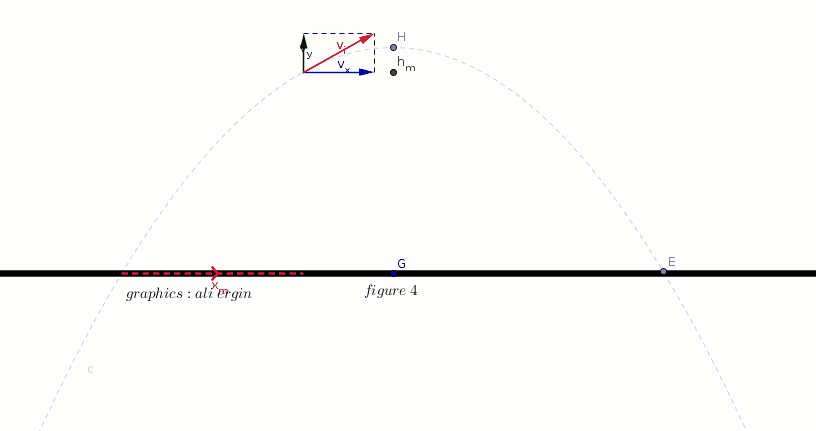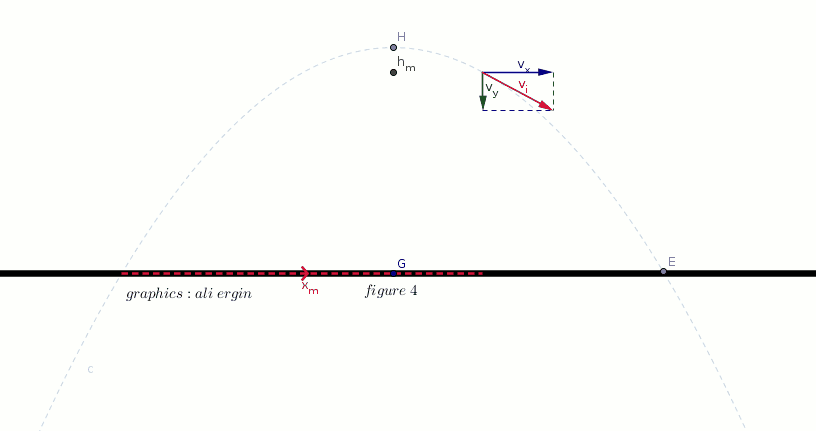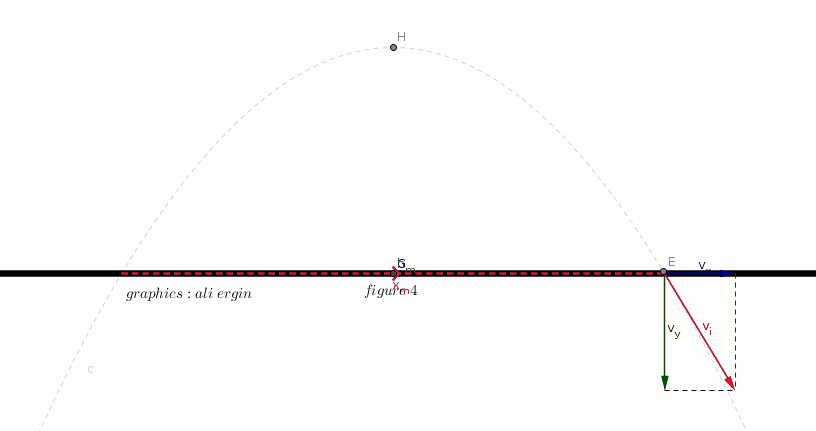
#"the horizontal position of object can be calculated by:"#
#x=color(green)(v_x)*color(red)(t)#
#x=color(green)(v_i*cos alpha)*color(red)(t)#
#"now; we can write "color(red)(t=t_t)#
#x=(v_i*cos alpha*(2*v_i*sin alpha))/g#
#"so "2*sin alpha*cos alpha=sin(2 alpha)#
#x=(v_i^2*sin(2alpha))/g#
#"where "v_i=29" m/s"" "alpha=((2pi)/3) #
#x=(29^2*sin(2*(2pi)/3))/(9.81)#
#x=(841*0.866)/(9.81)#
#x=74.24" m"#







