A projectile is shot from the ground at a velocity of #5 m/s# and at an angle of #(2pi)/3#. How long will it take for the projectile to land?
1 Answer
Explanation:
Assuming the launch and landing points are at equal altitudes, we can use a kinematic equation to determine the flight time from the launch of the projectile to its maximum altitude (
We know that when an object is in free fall, the acceleration is equal to
Because the projectile is launched at an angle, we will need to break the velocity up into components. This can be done using basic trigonometry.
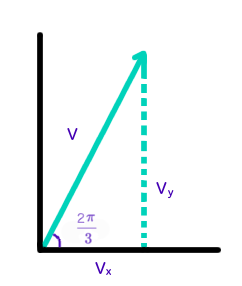
Where
We will only require the
We can now calculate the rise time of the projectile.
The total flight time is then

