Question

A projectile is shot from the ground at a velocity of `6 m/s` and at an angle of `(5pi)/6`. How long will it take for the projectile to land?

Answer 1

We separate the motion into vertical and horizontal and solve for the vertical position as a function of time, finding that the object returns to the ground at `t=0.61s`

Explanation:

There are many ways to answer this question, for example, we could solve for the full equation of motion in two dimensions and then find the time for the object to complete its parabolic path:

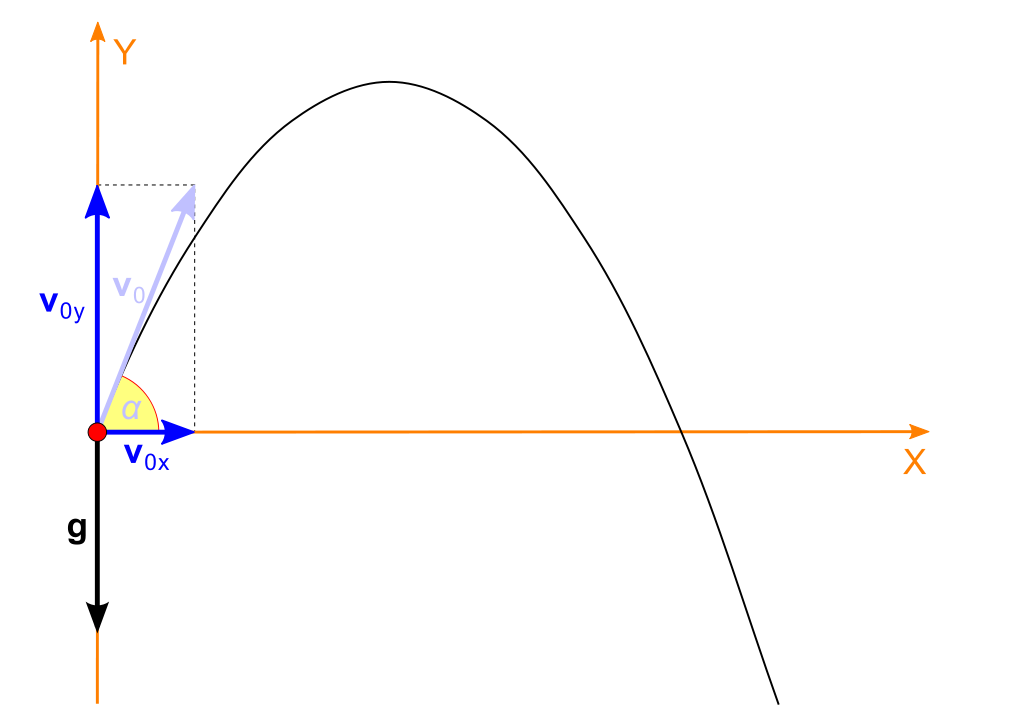
But this is more work than we need to do. We can separate the vertical and horizontal components of the motion and treat them separately. In our case, we only care about the vertical component and we'll completely ignore the horizontal .

What we need is an expression for the vertical position of the object so that we can determine when it returns to the ground, which we'll call `y=0`. The expression we are looking for is for an object under constant acceleration, `g`, and with an initial velocity, `v_(oy)` and position, `y_o`. We can use the equation for the position of an object under constant acceleration:

`y(t) = y_o + v_(oy)t-1/2 g t^2`

where `g = 9.8m//s^2` is the acceleration due to gravity. Of course, the object started on the ground, so `y_o=0` . Now we just need the initial vertical velocity. The angle (assuming measured from the ground) is `5 pi //6` (take a second to plot this and you may find it is a strange angle in that it's a low elevation on the other side of vertical), so the `y` component of this is given by:

`v_(oy) = sin((5 pi)/6)v_o = 1/2 6m//s = 3m//s`

Putting this into our equation for `y` and setting it equal to zero (the position on the ground) we get:

`0=3 m/s * t - 4.9 m / s^2 * t^2`

If we eliminate `t=0` as a possible solution we can divide by `t` to get

`4.9 m/s^2 t = 3m/s implies t=0.61s`

follow this link for more detail