Question

A radioactive element has a half-life of 5 years. If you leave a 2 g sample of this element under your chemistry desk for 15 years, what mass will remain undecayed?

Answer 1

`"0.25 g"`

Explanation:

So, you know that your radioactive element has a nuclear half-life of `5` years.

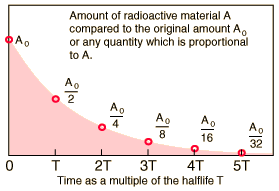
As you know, a radioactive isotope's half-life tells you the time needed for half of an initial sample to undergo radioactive decay.

If you start with an initial sample `A_0`, you can say that you'll be left with

• `A_0 * 1/2 ->` after one half-life
• `A_0/2 * 1/2 = A_0/4 ->` after two half-lives
• `A_0/4 * 1/2 = A_0/8 ->` after three half-lives
  `vdots`

and so on. This means that you can express a relationship between the Initial sample of the radioactive isotope, `A_0`, and the amount that remains undecayed, `A`, in terms of how many half-lives pass in a given period of time

`color(blue)(A = A_0 * 1/2^n)" "`, where

`n` - the number of half-lives

In your case, you can say that

`n = (15 color(red)(cancel(color(black)("years"))))/(5color(red)(cancel(color(black)("years")))) = 3`

This means that you'll be left with

`A = A_0 * 1/2^3 = 1/8 * A_0`

Therefore, your original sample will be down to `1/8"th"` of its initial value after the passing of `15` years

`A = 1/8 * "2 g" = color(green)("0.25 g")`

I'll leave the answer rounded to two sig figs.