A right triangle has sides A, B, and C. Side A is the hypotenuse and side B is also a side of a rectangle. Sides A, C, and the side of the rectangle adjacent to side B have lengths of #5 #, #2 #, and #4 #, respectively. What is the rectangle's area?
1 Answer
Sep 1, 2017
Explanation:
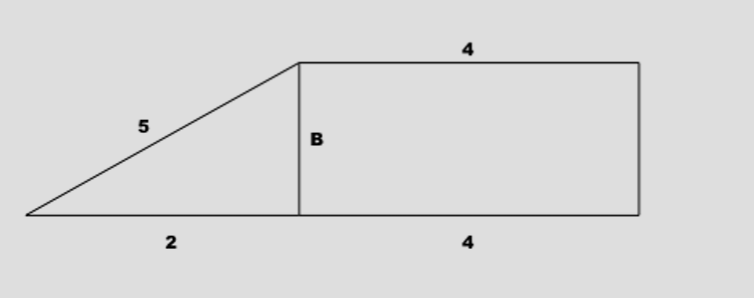
This is an image I created using the information you provided.
First, let's find the length of side
Both of the widths of the rectangle should be labelled
The area of the rectangle will be the product of its length and width:
Therefore, the area of the rectangle is

