Question

A right triangle's leg is 9 and the hypotenuse is 15, what is the other leg s length?

Answer 1

The length of the other leg is 12

Explanation:

The Pythagorean theorem is:

`a^2+b^2=c^2" [1]"`

Where "a" and "b" legs of the triangle and side "c" is the hypotenuse.

We are given that the triangles right leg is 9 and the hypotenuse is 51. Because addition is commutative, it does not matter whether we choose to assign "a" or "b" the known length; I shall choose "a":

Let `a = 9` and `c = 15`

Substitute this into equation [1]:

`9^2 + b^2 = 15^2`

Compute the squares:

`81+b^2=225`

Subtract 81 from both sides:

`b^2=144`

Square root both sides:

`b = +-12`

Discard the negative length:

`b = 12`

The length of the other leg is 12

Answer 2

The second leg's length is `12`.

Explanation:

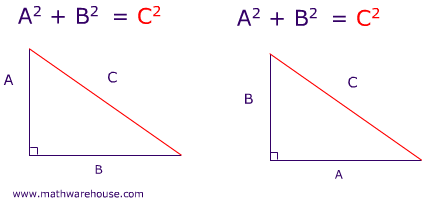
We'd use the pythagorean theorem to solve for the other leg's length. As the image suggests, we'd use the theorem, `a^2+b^2=c^2`.

If one leg is `9`, that's our `a` value.
If the hypotenuse is `15`, that's our `c` value.
Now we just have to find the `b` value.

Plugging in the variables, `9^2+b^2=15^2`.

`9^2=81`.
`15^2=225`.

`81+b^2=225`. Subtract `81` from both sides.

`b^2=144`. Square root both sides.

`sqrt(b^2)=b` and `sqrt(144)=12`, so `b=12`