A sample of a gas has a volume of 2.0 liters at a pressure of 1.0 atmosphere. What will the pressure be when the volume increases to 4.0 liters at constant temperature?
1 Answer
Explanation:
The idea here is that the pressure of a gas and the volume it occupies have an inverse relationship when the temperature and the number of moles of gas, i.e. the amount of gas present in the sample, remain constant
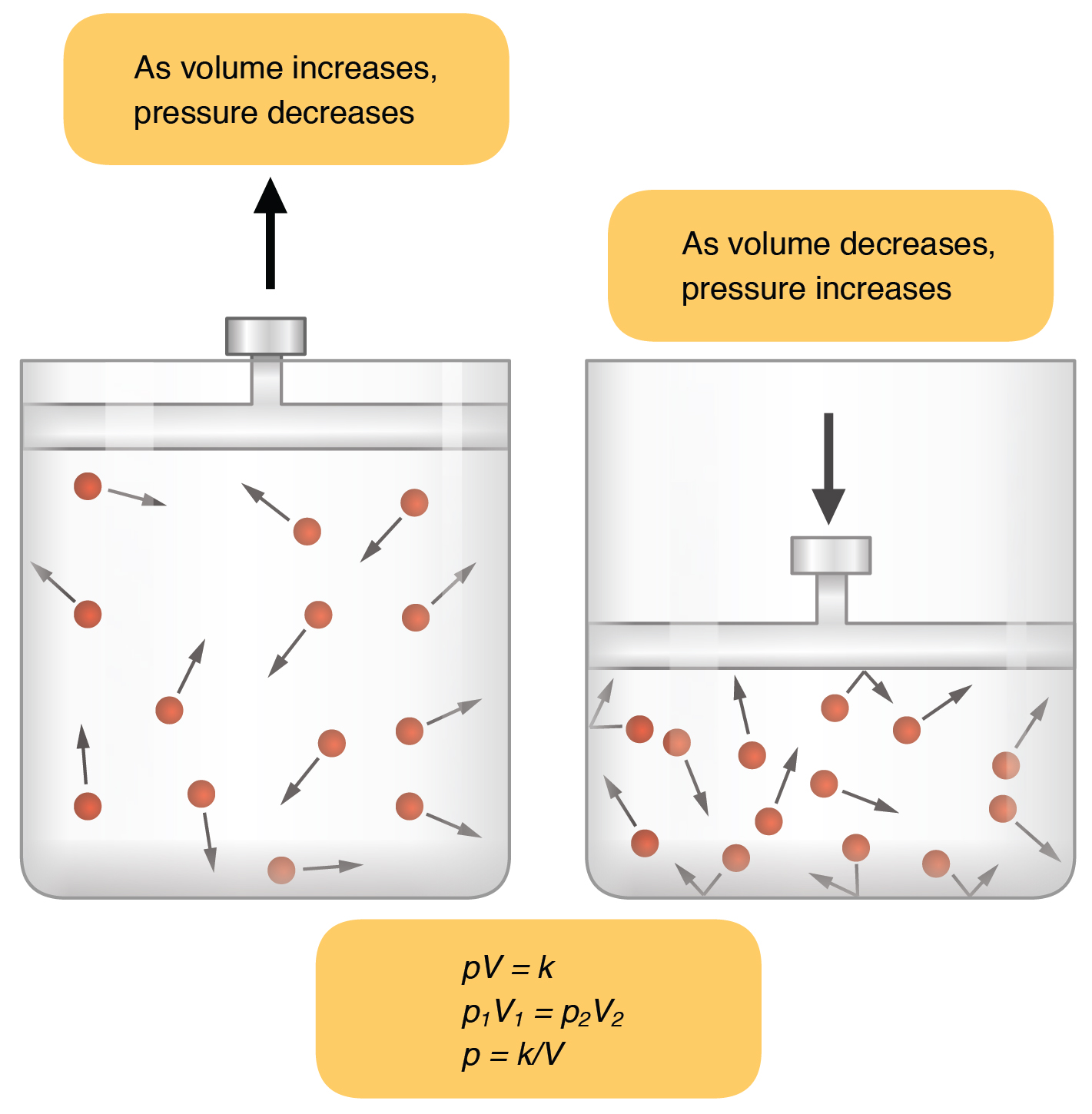
Simply put, when the temperature and the number of moles of gas are constant, a decrease in the volume of the gas will cause an increase in its pressure and an increase in the volume of the gas will cause a decrease in its pressure.
In your case, you know that the volume is increasing
#"2.0 L " -> " 4.0 L"#
so you should expect the volume to decrease
#"1.0 atm " > " P"_2#
Your tool of choice here will be this equation
#color(blue)(ul(color(black)(P_1V_1 = P_2V_2)))#
Here
#P_1# and#V_1# represent the pressure and volume of the gas at an initial state#P_2# and#V_2# represent the pressure and volume of the gas at a final state
Rearrange to solve for
#P_1V_1 = P_2V_2 implies P_2 = V_1/V_2 * P_1#
and plug in your values to find
#V_2 = (2.0 color(red)(cancel(color(black)("L"))))/(4.0color(red)(cancel(color(black)("L")))) * "1.0 atm" = color(darkgreen)(ul(color(black)("0.50 atm")))#
The answer is rounded to two sig figs.

