A sample of oxygen gas occupies a volume of 365.2 L. When the volume is increased to 478.2 L, the new pressure is 24.13 atm. What was the original pressure?
1 Answer
Explanation:
Before doing any calculation, try to predict what the original pressure of the gas must have been relative to its new value of
So, no mention is made about temperature or number of moles of gas, which means that you can consider them constant.
When temperature and pressure are kept constant, volume and pressure have an inverse relationship - this is known as Boyle's Law.
Simply put, when volume Increases, pressure decreases, and when volume decreases, pressure increases.
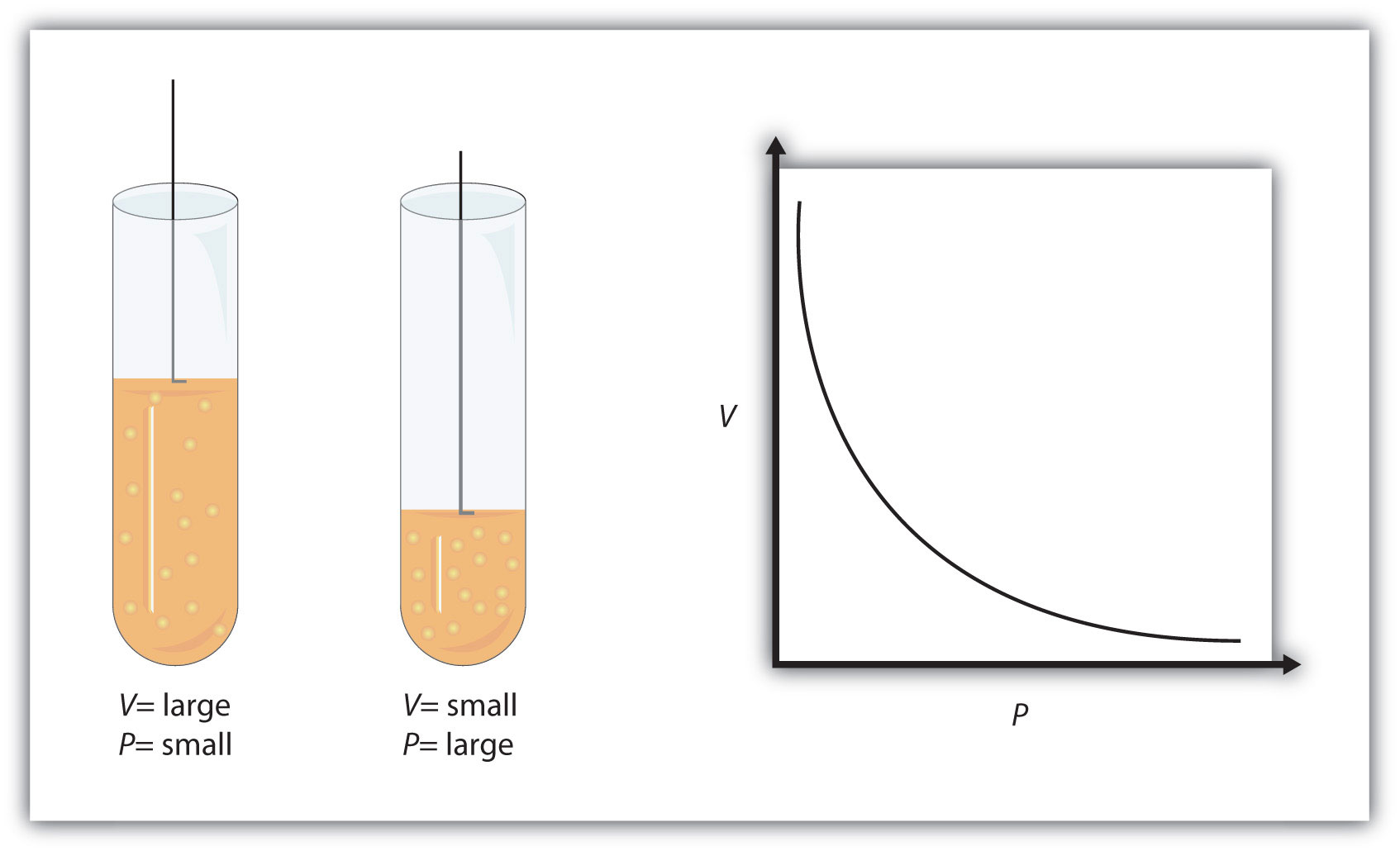
This happens because, as you know, gas pressure is caused by the collisions between the gas molecules and the walls of the container. The more powerful and more frequent these collisions, the higher the gas pressure.
Temperature is actually a measure of the gas molecules' average kinetic energy. When volume is increased at constant temperature, the force with which the molecules are hitting the wall is kept constant.
However, the larger volume means more room for these molecules to move around in, which in turn means less frequent collisions with the walls of the container
Since volume was increased for this gas, you can expect the final pressure to be lower than the initial pressure.
With this in mind, use the equation described by Boyle's Law to find the actual value of the initial pressure.
#color(blue)(P_1 * V_1 = P_2 * V_2)" "# , where
Plug in your values and solve for
#P_1 * V_1 = P_2 * V_2 implies P_1 = V_2/V_1 * P_2#
#P_1 = (478.2color(red)(cancel(color(black)("L"))))/(365.2 color(red)(cancel(color(black)("L")))) * "24.13 atm"#
#P_1 = color(green)("31.60 atm")#
As predicted, the pressure decreased as a result of the increase in volume.

