Question

A solid consists of a cone on top of a cylinder with a radius equal to that of the cone. The height of the cone is `9` and the height of the cylinder is `12`. If the volume of the solid is `24 pi`, what is the area of the base of the cylinder?

Answer 1

`8/3 pi`

Explanation:

Consider the solid

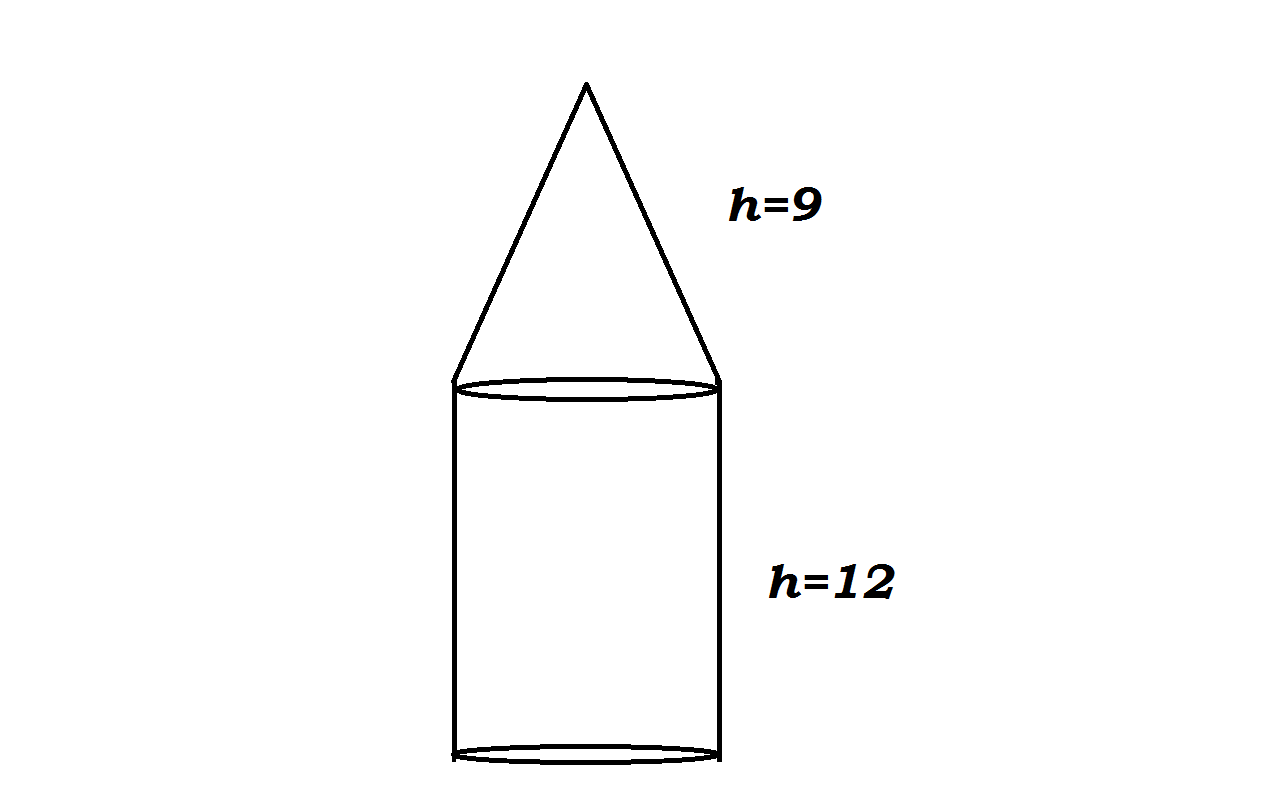
We can say that the volume of the solid equals the sum of the volume of the cone and the cylinder

`color(blue)(V_(cy)+V_(co)=24pi`

Volume of cylinder`=color(purple)(pir^2h`

Volume of cone`=color(indigo)(1/3pir^2h`
(`1/3` of the volume of cylinder)

Area of the base (the base is a circle)`=color(orange)(pir^2`

`n` `ot` `e` `:pi=22/7`

If you take a closer look at the formula, you could see `pir^2` appearing in both. So,let `pir^2` be `w`

`color(orange)(pir^2=w`

`rarrwh+1/3wh=24pi`

`rarrw*12+1/3*w*9=24pi`

`rarrw*12+1/cancel3^1*w*cancel9^3=24pi`

`rarr12w+3w=25pi`

`rarr15w=24pi`

`color(green)(rArrw=(24pi)/15=8/3pi`

(area of the base)