A solid consists of a cone on top of a cylinder with a radius equal to that of the cone. The height of the cone is #60 # and the height of the cylinder is #15 #. If the volume of the solid is #70 pi#, what is the area of the base of the cylinder?

Question

1023 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-08-26T16:06:34

#"Area of Base of cylinder"=2pi#

#"The Diagram:"#

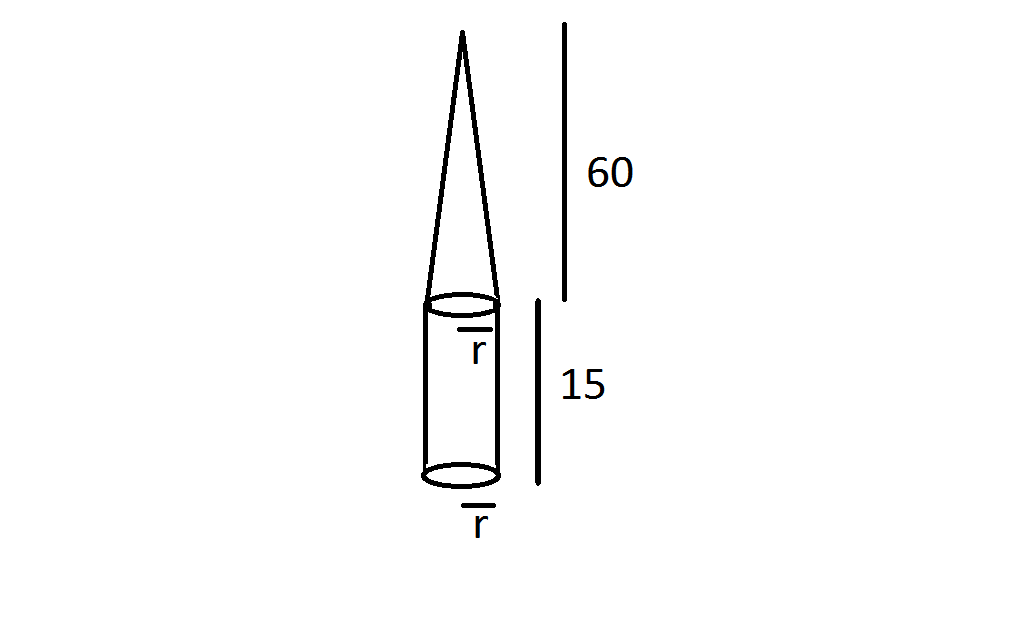
enter image source here

#color(blue)("We know that the volume of the whole solid is"# #70pi#

#(or)#

#color(red)("The sum of the volumes of the cone and cylinder is "# #70pi#

#"Now lets set up an equation for solving the question"#

#color(brown)("Volume of cone"=1/3 pir^2h=v_1#

#color(brown)("Volume of cylinder"=pir^2h=v_2#

#"(Where "h" is the height and "r" is the radius)"#

#"Known values of the variables":#

#color(violet)(h# #color(violet)("of"# #color(violet)(v_1=60#

#color(violet)(h# #color(violet)("of"# #color(violet)(v_2=15#

#"We need to find the value of"# # pir^2# #"which is the base"#

#:.color(orange)(v_1+v_2=70pi#

#rarr1/3pir^2h+pir^2h=70pi#

#rarr1/3pir^(2)60+pir^(2)15=70pi#

#rarr1/cancel3^1pir^(2)cancel60^20+pir^(2)15=70pi#

#rarrpir^(2)20+pir^(2)15=70pi#

#"Rewrite the equation"#

#rarr20pir^(2)+15pir^(2)=70pi#

#rarr35pir^2=70pi#

#rarrpir^2=(cancel70^2pi)/cancel35^1#

#rArrcolor(green)(pir^2=2pi#