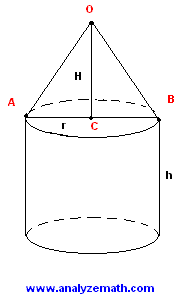
A solid consists of a cone on top of a cylinder with a radius equal to that of the cone. The height of the cone is #9 # and the height of the cylinder is #12 #. If the volume of the solid is #72 pi#, what is the area of the base of the cylinder?

Question

1398 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-12-22T13:18:04

Area of the base of the cylinder is 15.0796

Let V be the volume of the solid = #72 pi#

Volume of the object V = volume of cylinder + volume of cone

Given cylinder height #h = 12#, cone height #H = 9#

Volume of cylinder #= pi * r^2 * h#

Volume of cone #= (1/3) pi * r^2 * H#

#V = pi r^2 h + (1/3) pi r^2 H#

#96 pi = pi r^2 (h + (1/3)H)#

#r^2 = (72 cancel(pi)) / (cancel(pi) (12 + (1/3)9))#

#r^2 = 72/15#

Area of base of cylinder #A = pi r^2 = pi * (72/15) = 15.0796#

enter image source here