Question

A solid consists of a cone on top of a cylinder with a radius equal to that of the cone. The height of the cone is `33` and the height of the cylinder is `17`. If the volume of the solid is `168 pi`, what is the area of the base of the cylinder?

Answer 1

`6pi`

Explanation:

Consider the diagram

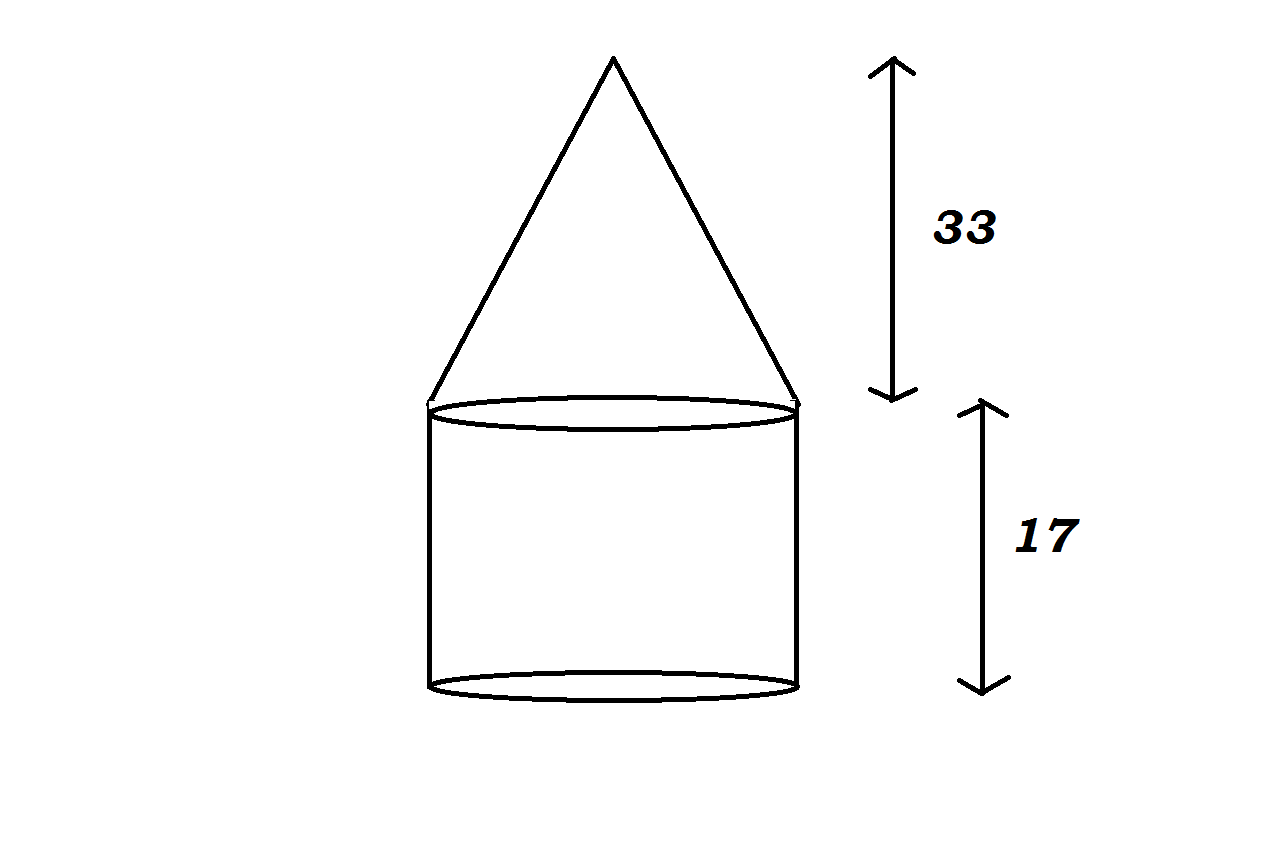
Note: `color(brown)(pi=22/7,V=volume,h=height`

Remember the formulas

`color(purple)(V_(con)=1/3pir^2h`

`color(purple)(V_(cyl)=pir^2h`

`color(purple)(Area_(base)=pir^2`

And `r` is the radius of the base (circle)

We know that the volume of the whole solid is `168pi`

Our aim is to find Area of base (`pir^2`)

And we could see that `pir^2` is present in both of the volume formulas

So, consider `pir^2` as `a`

`rarr1/3*a*33+a*17=168pi`

`rarr1/cancel3^1*a*cancel33^11+a*17=168pi`

`rarra*33+a*17=168pi`

`rarr28a=168pi`

`rarra=168/28pi`

`color(green)(rArra=6pi`

Source of image: paint (my drawing)

And,if you don't like this drawing and want to change it, your changes are welcome