A solid consists of a cone on top of a cylinder with a radius equal to that of the cone. The height of the cone is #33 # and the height of the cylinder is #13 #. If the volume of the solid is #256 pi#, what is the area of the base of the cylinder?
2 Answers
Explanation:
A Conical Volume is given by:
A Cylindrical Volume is given by:
Circular Area (base of cylinder)
Total solid volume =
Explanation:
Let's consider the diagram
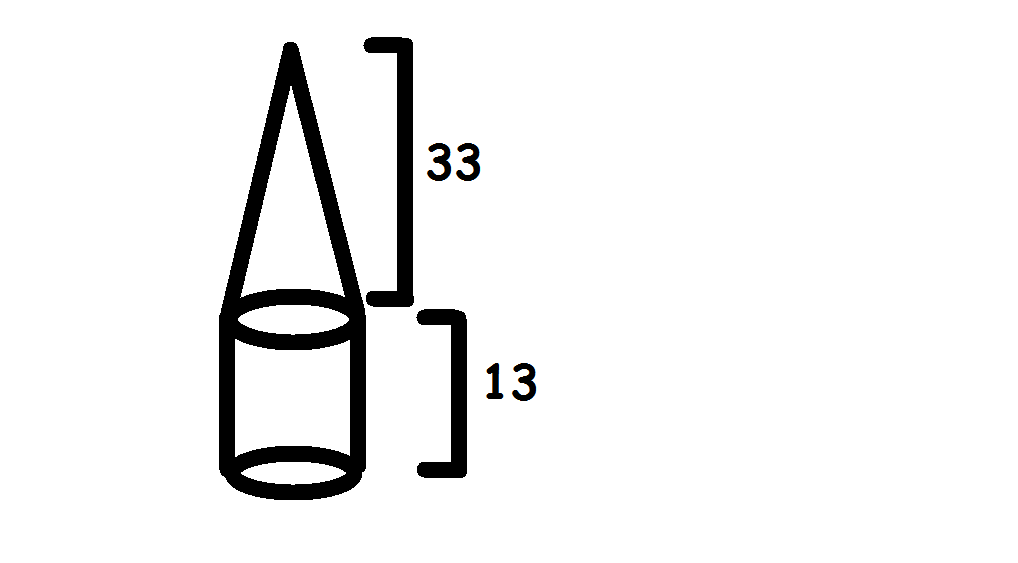
We need to find the area of the base of the cylinder, which is a circle. The area of a circle is given by
#color(blue)("Area of circle"=pir^2#
Where
The total volume of the solid is
Therefore,
#color(purple)("Volume of cone"+"Volume of cylinder"=256pi #
We use the formulas
#color(orange)("Volume of cone"=1/3pir^2#
#color(orange)("Volume of cylinder"=pir^2h#
Where,
Now, Let's find the area of the base


