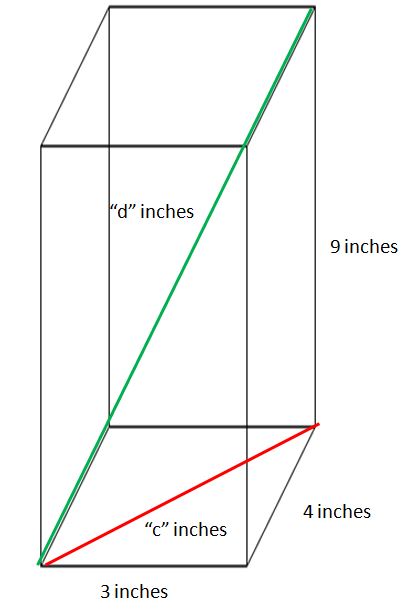
First, we can use the Pythagorean Theorem to find the length of the #color(red)(red)# line labelled ["c" inches]. The Pythagorean Theorem states for a right triangle, which the sides of a rectangle and the diagonal form, #a^2 + b^2 = c^2# where #a# and #b# are legs of the triangle and #c# is the hypotenuse.
Substituting for #3# for #a# and #4# for #b# and solving for #c# gives:
#3^2 + 4^2 = c^2#
#9 + 16 = c^2#
#25 = c^2#
#sqrt(25) = sqrt(c^2)#
#5 =c#
#c = 5#
We can now solve for the length of the #color(green)(green)# line which is also the length of the straw. Again, we can use the Pythagorean Theorem substituting #5# for #a# and #9# for #b# and again solving for #c#:
#5^2 + 9^2 = c^2#
#25 + 81 = c^2#
#106 = c^2#
#sqrt(106) = sqrt(c^2)#
#10.296 = c#
#c = 10.296# rounded to the nearest thousandth.
The length of the straw is #sqrt(106)# inches or #10.296# inches rounded to the nearest thousandth.

