Question

A triangle has corners at points A, B, and C. Side AB has a length of `35`. The distance between the intersection of point A's angle bisector with side BC and point B is `14`. If side AC has a length of `36`, what is the length of side BC?

Answer 1

The right answer for this problem is given by @shwetank-m (Shwetank Mauria). In explanation I give an answer for the case in which the segment between point A and the intersection with side BC is 14.

Explanation:

Refer to the figure below

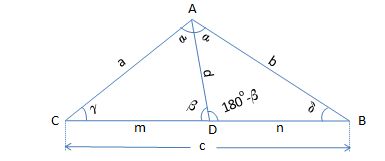
Applying the Law of Sines
to `triangle_(ACD)`

`a/sin beta=m/sin alpha`

to `triangle_(ABD)`

`b/sin(180^@-beta)=n/sin alpha` => `b/sin beta=n/sin alpha`

So
`a/b=m/n` => `m=(a/b)n`

NOTE 1
WHAT IS WRITTEN ABOVE STANDS JUST AS PREAMBLE TO THE ANSWER BY @shwetank-m, WHEN -> N=14

NOTE 2
WHAT IS WRITTEN BELOW IS THE ANSWER WHEN -> D=14

Applying the Law of Cosines to both the aforementioned triangles

`m^2=a^2+d^2-2ad*cos alpha` => `m^2-a^2-d^2=-2ad*cos alpha`
`n^2=b^2+d^2-2bd*cos alpha` => `n^2-b^2-d^2=-2bd*cos alpha`

Dividing the two last expressions and substituting `m` we get
`(a^2/b^2n^2-a^2-d^2)/(n^2-b^2-d^2)=a/b`
`a^2/bn^2-b(a^2+d^2)=an^2-a(b^2+d^2)`
`(a^2/b-a)n^2=-a(b^2+d^2)+b(a^2+d^2)`
`a/b(b-a)n^2=a(b^2+d^2)-b(a^2+d^2)`
`n=sqrt(b/a*(a(b^2+d^2)-b(a^2+d^2))/(b-a))`

For `a=35`, `b=36` and `d=14`

`n=sqrt(36/35*(35(36^2+14^2)-36(35^2+14^2))/(36-35))`
`n=sqrt(36/35*(35*1492-36*1421)/1)=sqrt(36/35*1064)=12sqrt(38/5)~=33.08`
=>`m=35/36*12sqrt(38/5)=35/3sqrt(38/5)~=32.16`

So
`BC=c=m+n=35/3sqrt(38/5)+12sqrt(38/5)=71/3sqrt(38/5)~=65.24`

Answer 2

`BC=28.4`

Explanation:

Using angle bisector theorem (in the figure drawn by Rui D.), we have

`a/b=m/n` or `36/35=m/14`

Hence `m=36/35xx14=72/5=14.4`

Hence `BC=14.4+14=28.4`