A triangle has corners at points A, B, and C. Side AB has a length of 9 . The distance between the intersection of point A's angle bisector with side BC and point B is 6 . If side AC has a length of 8 , what is the length of side BC?
1 Answer
May 19, 2017
Explanation:
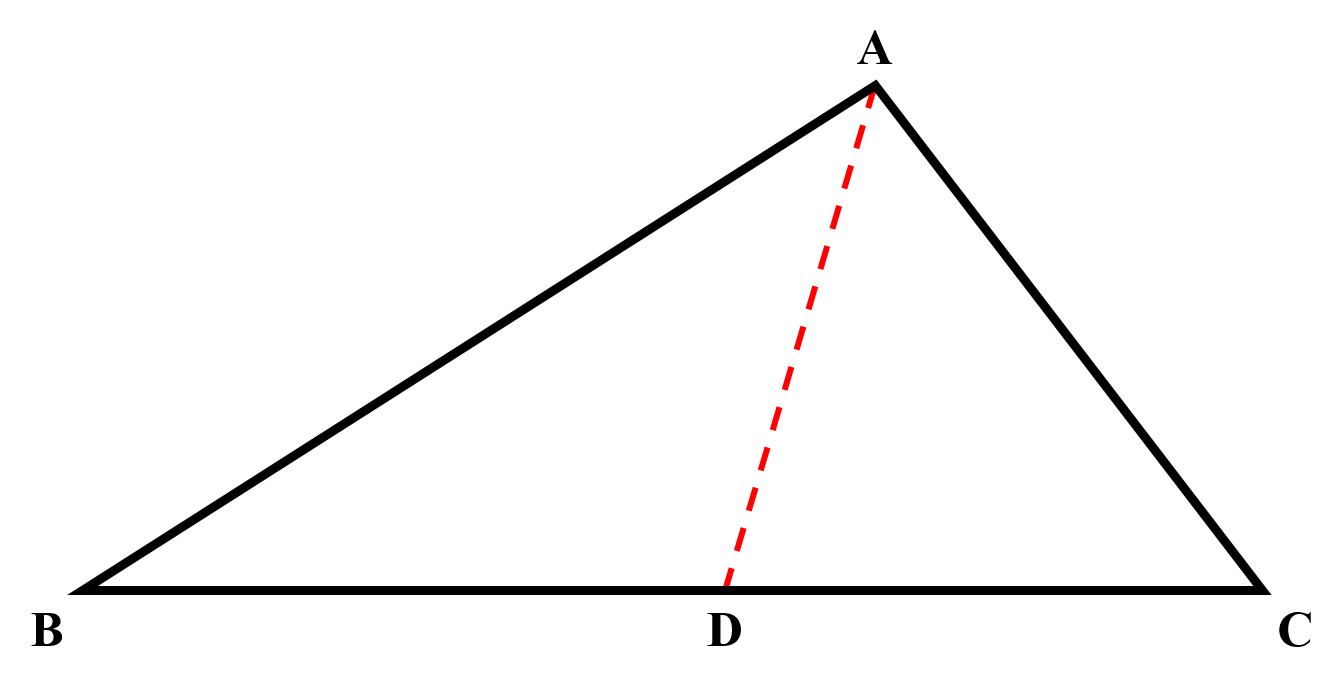
Consider this image where
Triangles have a property related to angle bisectors called the angle bisector theorem :-
That if
For proofs of this theorem visit this link.
I have gone through both the proofs and found them to be correct.
You can also watch this video.
Now, in this question,

