A triangle has sides A, B, and C. Sides A and B are of lengths #2# and #1#, respectively, and the angle between A and B is #(5pi)/12 #. What is the length of side C?
1 Answer
Apr 9, 2018
Explanation:
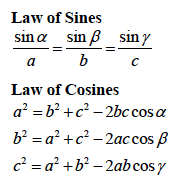
As per the Law of Cosines,
As length of side c cannot be negative,
