A triangle has sides A, B, and C. Sides A and B are of lengths #2# and #4#, respectively, and the angle between A and B is #(7pi)/8 #. What is the length of side C?
1 Answer
Dec 19, 2016
c=5.8737
Explanation:
The figure explaining the given data is given below:
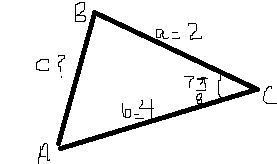
To find side 'c', Cosine rule would apply in this case. Cosine rule says that
Cos C=
c=5.8737
