A triangle has sides A, B, and C. Sides A and B are of lengths #2# and #5#, respectively, and the angle between A and B is #pi/12#. What is the length of side C?

Question

1357 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-01-27T10:22:01

#C ~~4.4#

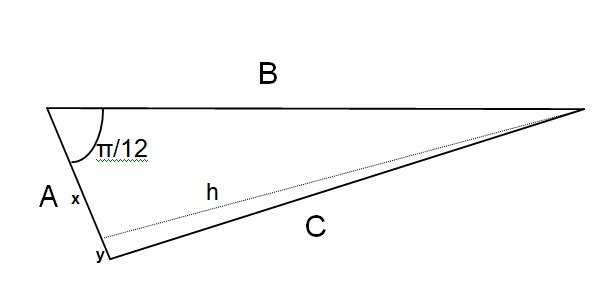
Sketch
Use the trigonometric relationships e.g. sine = opposite /hypotenuse
#A = x + y#

#x/B = cos(pi/12)#

#:. x= Bcos(pi/12) = 5cos(pi/12)#

Similarly #h = 5sin(pi/12)#

#y = A - x = 2 - 5cos(pi/12)#

Using Pythagoras, #C^2 = h^2 + y^2#

:.#C^2 = (5sin(pi/12))^2 +(2-5cos(pi/12))^2#

#C^2 = 25sin^2(pi/12) +4 - 10cos(pi/12) +25cos^2(pi/12)#

#C^2 = 25(sin^2(pi/12) +cos^2(pi/12)) +4 -10cos(pi/12) #

Using the fact that #sin^2(theta) + cos^2(theta) = 1# this is now

#C^2 = 25 + 4 - 10cos(pi/12) =29 - 10cos(pi/12)#

#C~~ sqrt(29-9.659) ~~4.4#