A triangle has sides A, B, and C. Sides A and B are of lengths #5# and #2#, respectively, and the angle between A and B is #(11pi)/12 #. What is the length of side C?
1 Answer
Dec 19, 2015
Use the Law of Cosines.
The angle between sides
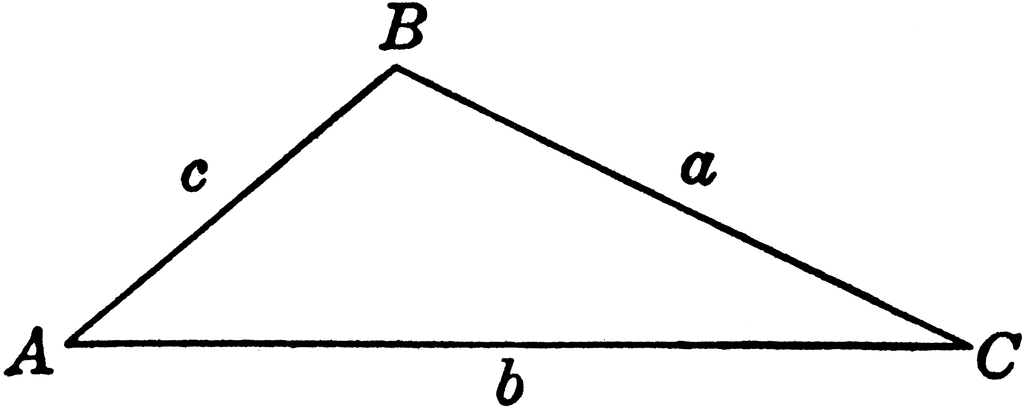
Plug in what you know.
Thus, this can be simplified and plugged into a calculator (remember to be in radian mode.

