A triangle has sides A, B, and C. Sides A and B are of lengths #9# and #3#, respectively, and the angle between A and B is #pi/6#. What is the length of side C?

Question

1397 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-01-29T12:09:30

#C~~6.575#

Let the perpendicular height of the triangle be #h#. This intersects side #A# so that lengths #x# and #y# add up to #A#
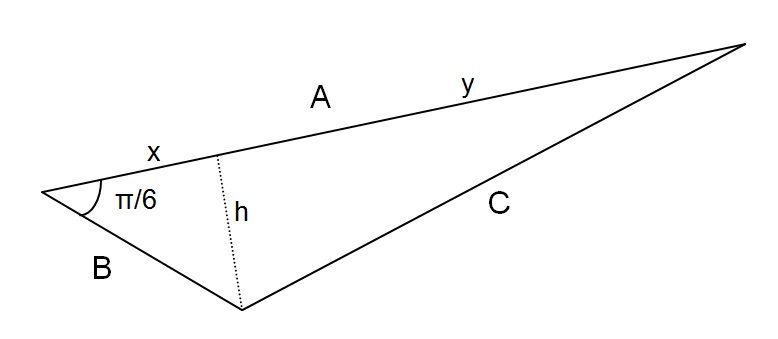
Sketch
#A =9#
#B = 3#

#sin(pi/6) = h/3#
#:. h = 3sin(pi/6) = 3*0.5 = 1.5#

#cos(pi/6) = x/3#
#:.x = 3cos(pi/6)#

#y=9 - 3cos(pi/6)#

Let the angle between #A# and #C# be #theta#. Then
#tantheta =h/y = 1.5/(9-3cos(pi/6))#

#theta =tan^-1(1.5/(9-3cos(pi/6)))#

#h/C = sintheta#
#:. C = 1.5/sintheta#

From here it is just a lot of grunt work with a calculator to get the length.

#C~~6.575#