Question

A triangle with the hypotenuse measuring 8, and the short leg measuring 5, and the the long leg measuring 7. How do you find the angles C the top angle, B the lower right angle, A the left angle?

Answer 1

Ignoring the (false) implication that we are dealing with a right angled triangle, we can use the Law of Cosines to determine the 3 angles

Explanation:

I have assumed that the triangle looks like:

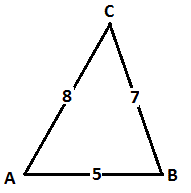
The reference to a hypotenuse implies a right-angled triangle but based on the Pythagorean Theorem this is clearly false.

The Law of Cosines for a triangle with sides `a, b, c` and corresponding opposite angles `A, B, C` is
`color(white)("XXX")c^2=a^2+b^2-2ab*cos(C)`

which can be re-arranged as:
`color(white)("XXX")cos(C)=((a^2+b^2)-c^2)/(2ab)`
or
`color(white)("XXX")C = arccos(((a^2+b^2)-c^2)/(2ab))`

and similarly for angles `A` and `B`

Plugging in the values for `a, b, c` (I would suggest using a calculator or spreadsheet), we get

In radians
`color(white)("XXX")A=1.047, B=1.427, C=0.667`

In degrees
`color(white)("XXX")A=60^@, B=81.8^@, C=38.2^@`