A truck pulls boxes up an incline plane. The truck can exert a maximum force of #3,500 N#. If the plane's incline is #(3 pi )/8 # and the coefficient of friction is #9/4 #, what is the maximum mass that can be pulled up at one time?
1 Answer
Explanation:
We can use Newton's second law to derive an equation for the maximum mass that the truck can pull up the incline at a time.
(I make the assumption that the truck and mass are always simultaneously on the incline and that whatever mechanism the used to connect the truck to the box is irrelevant.)
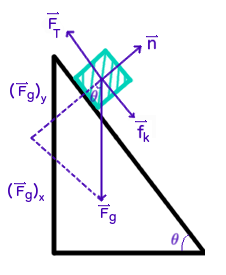
Force diagram for a box:
- Where
#vecn# is the normal force,#vecf_k# is the force of kinetic friction,#vecT# is the force of the truck, and#F_G# is the force of gravity, decomposed into its parallel (x, horizontal) and perpendicular (y, vertical) components.
We have the following information:
#|->mu_k=9/4# #|->theta=(3pi)/8# #|->F_T=3500"N"#
Relevant equations:
#f_k=mu_kn# #F_G=mg#
We can set up statements of the net force using the above information and diagram. Due to the nature of the situation, we will assume dynamic equilibrium, where the truck pulls the box at a constant velocity.
#sumF_x=F_T-f_k-F_(Gx)=0#
#sumF_y=n-F_(Gy)=0#
We will have to decompose the gravitational force
#sin(theta)="opposite"/"hypotenuse"#
#=>sin(theta)=F_(Gx)/F_G#
#=>F_(Gx)=F_Gsin(theta)#
#=>=mgsin(theta)#
Similarly, we can use the cosine function to show that
We now have:
#n=mgcos(theta)#
Therefore:
#color(darkblue)(F_T-mu_kmgcos(theta)-mgsin(theta)=0)#
We can rearrange the above equation to solve for
#=>color(darkblue)(m=F_T/(g(sintheta+mu_kcostheta)))#
Substituting in our known values:
#m=(3500"N")/((9.81"m"//"s"^2)(sin((3pi)/8)+9/4cos((3pi)/8))#
#=>m=199.885"kg"#
#=>color(darkblue)(m~~200"kg")#