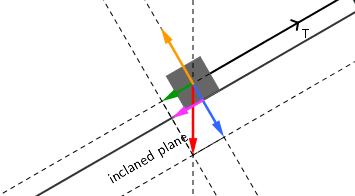
A truck pulls boxes up an incline plane. The truck can exert a maximum force of #3,500 N#. If the plane's incline is #(3 pi )/8 # and the coefficient of friction is #7/4 #, what is the maximum mass that can be pulled up at one time?
2 Answers
The mass is
Explanation:
Let the mass be
Force of truck is
The coefficient of friction is
Resolving in the direction patrallel to the plane
Explanation:
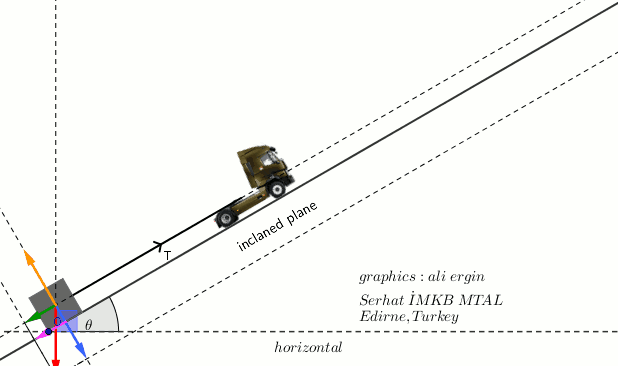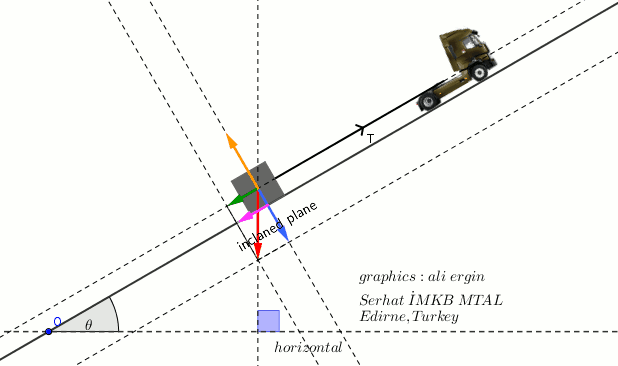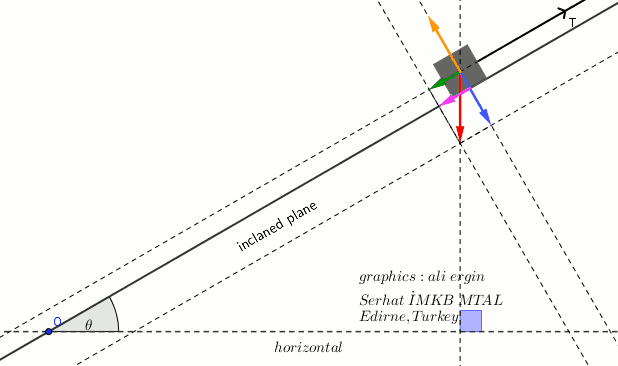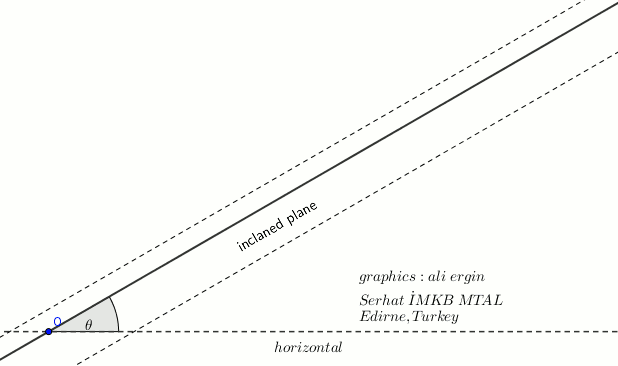
- the vector of weight is perpendicular to the horizontal surface.
- The vector of weight can be splitted into two component
- The component that is perpendicular to the inclined plane causes a Frictional force.
- The yellow vector represent the react force that it has applied inclined plane.
- The component that is parallel to the inclined plane causes sliding down..
- A Tension occurs on rope (T)