A uranium-235 sample starts with 200 atoms, and 700 million years later, there are 100 atoms. What is the half-life of uranium-235?

Question

A uranium-235 sample starts with 200 atoms, and 700 million years later, there are 100 atoms. What is the half-life of uranium-235?

1 Answer

Impact of this question

5845 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-06-27T11:06:47

$700 million years$ $"700 million years"$

Explanation:

The is a great example of a problem that wants to test your understanding of what exactly we mean when we say half-life.

The half-life of a radioactive nuclide, $t_{1/2}$ $t_"1/2"$ , is used to denote the time needed for a sample of said nuclide to decay to half of its initial size.

In other words, if you start with number of atoms and wait until half of them undergo radioactive decay, the period of time needed for this to happen is nuclide's half-life.

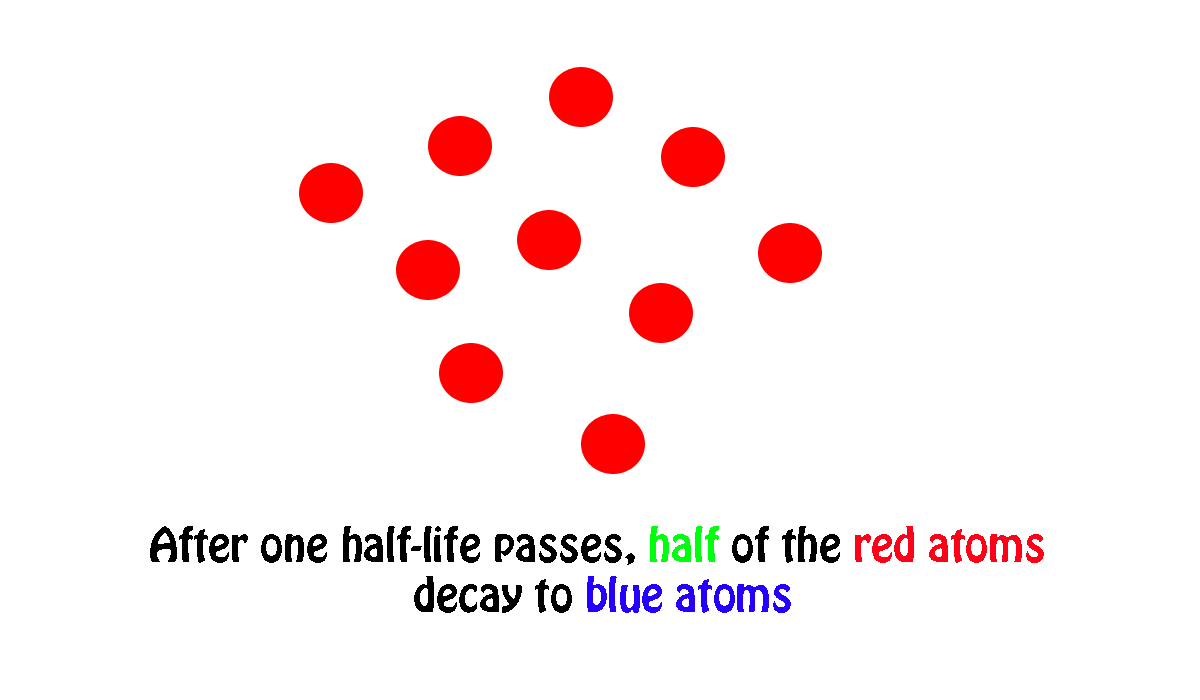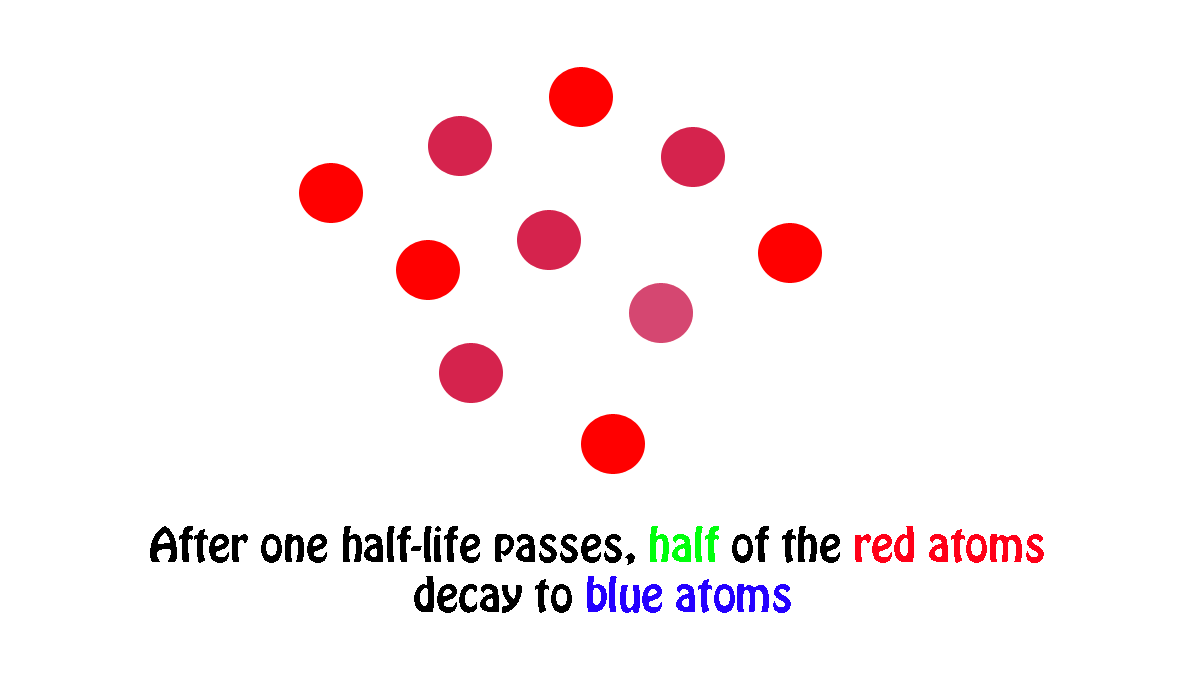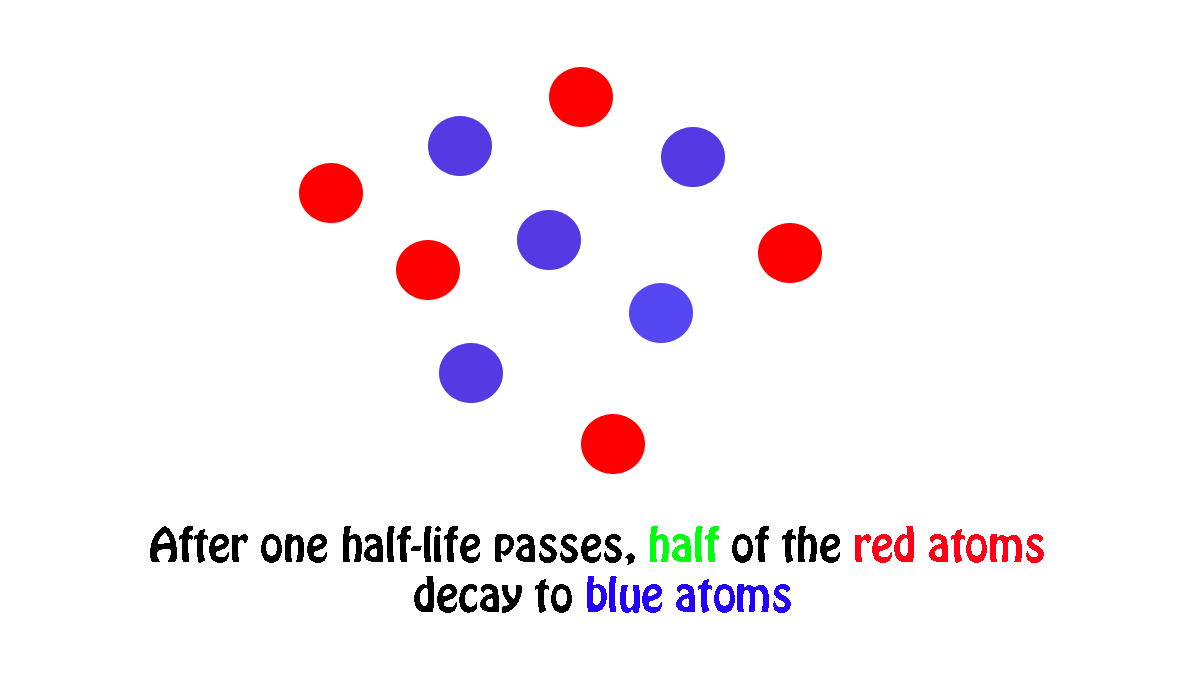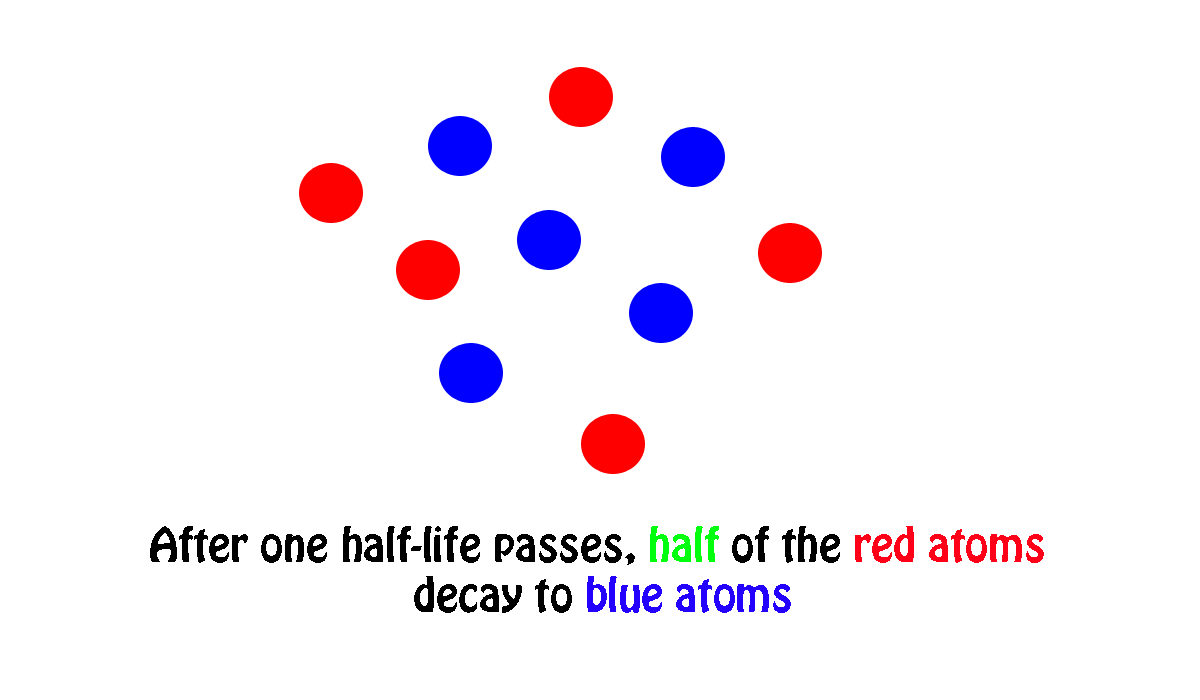My own work

In your case, a sample of $200$ $200$ atoms of uranium-235 needs $700$ $700$ million years to decay to $100$ $100$ atoms.

Since $100$ $100$ atoms represents half of the initial sample

$200 atoms \cdot \frac{1}{2} = 100 atoms$ $"200 atoms" * 1/2 = "100 atoms"$

it follows that the time needed for your sample to decay from $200$ $200$ to $100$ $100$ atoms represents the half-life of uranium-235.

Therefore, you can say that

$color(green)(|bar(ul(color(white)(a/a)color(black)(t_"1/2" = "700 million years")color(white)(a/a)|)))$

Science

Math

Humanities

... and beyond

A uranium-235 sample starts with 200 atoms, and 700 million years later, there are 100 atoms. What is the half-life of uranium-235?

1 Answer

Explanation:

Related questions

Impact of this question