A wagon wheel is placed against a wall. One point on the edge of the wheel is 5 inches from the ground and 10 inches from the wall. What is the radius of the wheel?
1 Answer
Explanation:
Acknowledgements to Stefan. V for this solution.
The trick here is the placement of the wheel.
Note that the circumference touches both the wall and the ground.
Check out this diagram
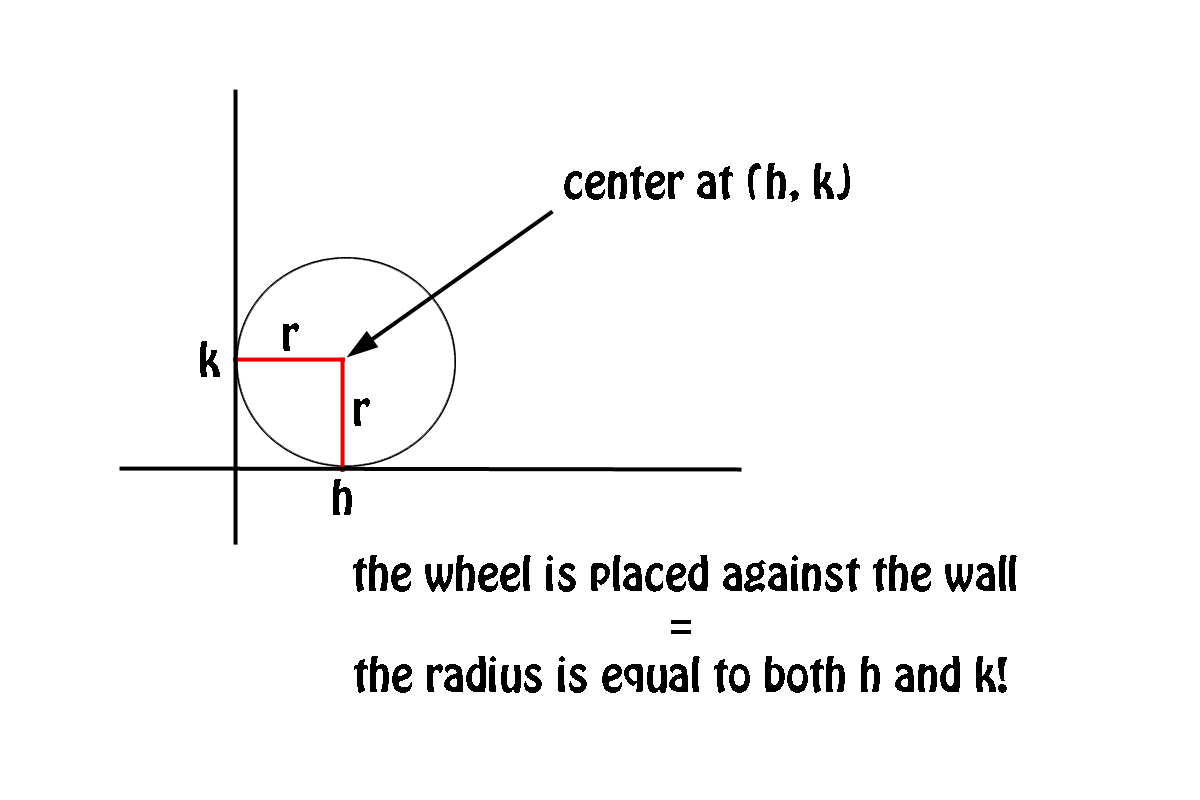
So if you start with the equation of a circle with the centre at
Use the fact that the wheel is touching both the wall and the ground at a distance equal to its radius from the centre to say that
This means that for any point
This gives:
Now it's just a matter of plugging in the point
The quadratic produces two solutions:
Reject x=5, as this is too small for the given point.
This is the required radius.
Thanks Stefan V.


