A water balloon is thrown by Sandra out of her dormitory window at an angle of 60o. It lands at the feet of Chris, who is standing a horizontal distance of 6.00 m from the building. If it takes 2.50 s to reach Chris’s feet ?

Question

how to determine the height h that Sandra threw it from.

5860 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2015-12-13T17:57:22

#20.2"m"#

The situation is like this:

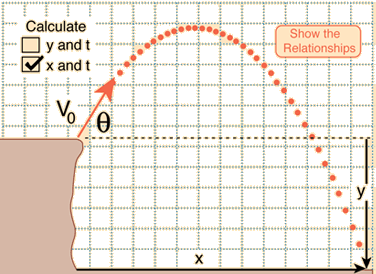hyperphysics.phy-astr.gsu.edu

In the convention I use, up is +ve, down is -ve.

#theta=60^@#

#x=6"m"#

The horizontal component of the velocity is constant so:

#vcos60=x/t#

#:.v=(x)/(tcos60)=6/(2.5xx0.5)=4.8"m/s"#

Now we can use:

#s=ut+1/2at^2#

Using the sign convention this becomes:

#h=vsinthetat-1/2"g"t^2#

#:.h=4.8xx0.866xx2.5-0.5xx9.8xx2.5^2#

#h=10.392-30.625=-20.233"m"#

This means that Sandra threw it from a height of #20.2"m"#