Question

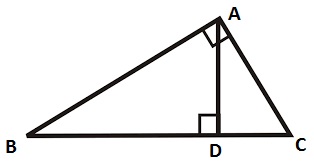
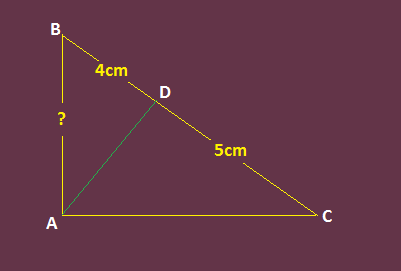
ABC is a right angle triangle. AD is drawn perpendicular to BC. If BC = 9cm, BD = 4 cm then find AB?

Answer 1

`AB=6`

Explanation:

As `AD` is drawn perpendicular to `BC` in right angled `DeltaABC`, it is apparent that `DeltaABC` is right angled at `/_A` as shown below (not drawn to scale).

As can be seen `/_B` is common in `Delta ABC` as well as `DeltaDBA` (here we have written two triangles this way as `/_A=/_D`, `/_B=/_B` and `/_C=/_BAD`) - as both are right angled (obviously third angles too would be equal) and therefore we have

`Delta ABC~~DeltaDBA` and hence

`(BC)/(AB)=(AB)/(BD)=(AC)/(AD)`..............(1)

therefore, we have `(BC)/(AB)=(AB)/(BD)` or

`AB^2=BCxxBD=9xx4=36`

Hence `AB=6`

Answer 2

Given that `DeltaABC` is right angled and `AD` is drawn perpendicular to `BC` . So `/_BAC` is right angle.

Given `BC = 9cm and BD =4cm-> CD = BC-BD=5cm`

In `Delta ABC and Delta ABD`

• `/_ABD=/_ABC`

• `/_ADB=/_BAC= "right angle"`

• `/_BAD=/_ACD ("remaining")`

So `Delta ABC and Delta ABD` are similar

Hence

`(AB)/(BC)=(BD)/(AB)`

`=>AB^2=BDxxBC=4xx9=36`

`=>AB=sqrt36cm=6cm`