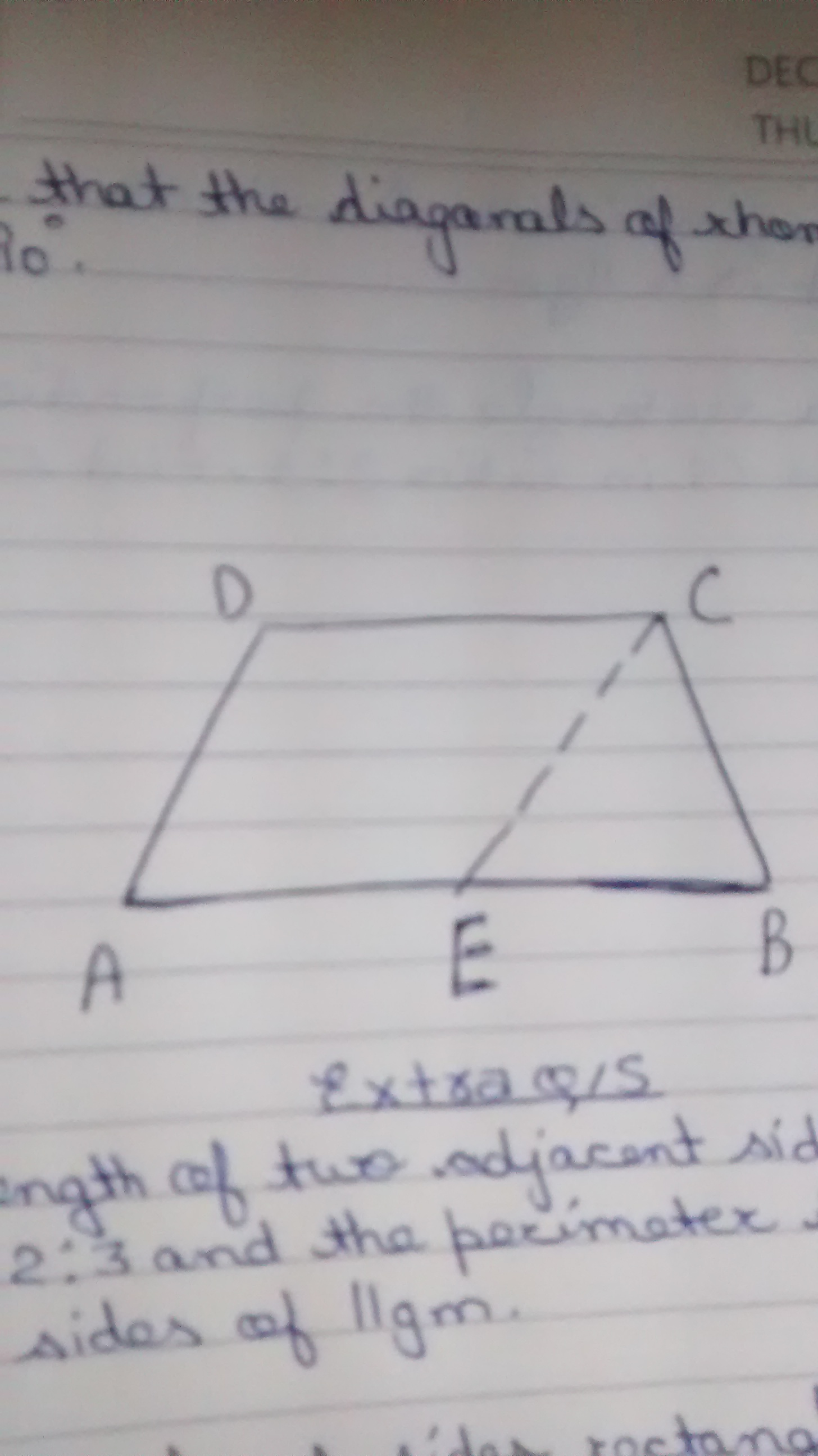
ABCD is a trep. with AB//DC and AD = BC. If AD is parallel to CE and angle A is 70 degrees.Find all the angles ? Diagram is given below.
1 Answer
See explanation.
Explanation:
Given:
(1) trapezoid
#ABCD#
(2)#bar(AB) " || " bar(CD)#
(3)#bar(AD) ~= bar(BC)#
(4)#bar(AD) " || " bar(CE)#
(5)#"m"angleA=70°#
We can immediately obtain
(6)
#"m"angle D = 110°#
because
(2) & (4) tell us that
(7)
#AECD# is a parallelogram
and thus
(8)
#bar(AD) ~= bar(EC)#
From (3) and (8) we get
(9)
#bar(BC) ~=bar(EC)#
(10)#triangleECB ~= triangle BCE#
and so
(11)
#angle CEB ~= angle B#
From (4), we get
(12)
#angle A ~= angle CEB#
This, together with (11) gives
(13)
#angle A ~= angle B#
(14)#"m"angle B =70°#
Just as
(15)
#"m"angle BCD =110°# .
From (11) and (14), we get
(16)
#"m"angle CEB = 70°#
and since
(17)
#"m"angle AEC = 110°#
(18)
#"m"angle ECD = 70°#
Finally, we use (15) and (18) to get
(19)
#"m"angle BCE = 40°# .

