An equilateral triangle is circumscribed about a circle of radius 10sqrt3. What is the perimeter of the triangle?
1 Answer
Sep 28, 2015
The perimeter of the triangle is 180 units.
Explanation:
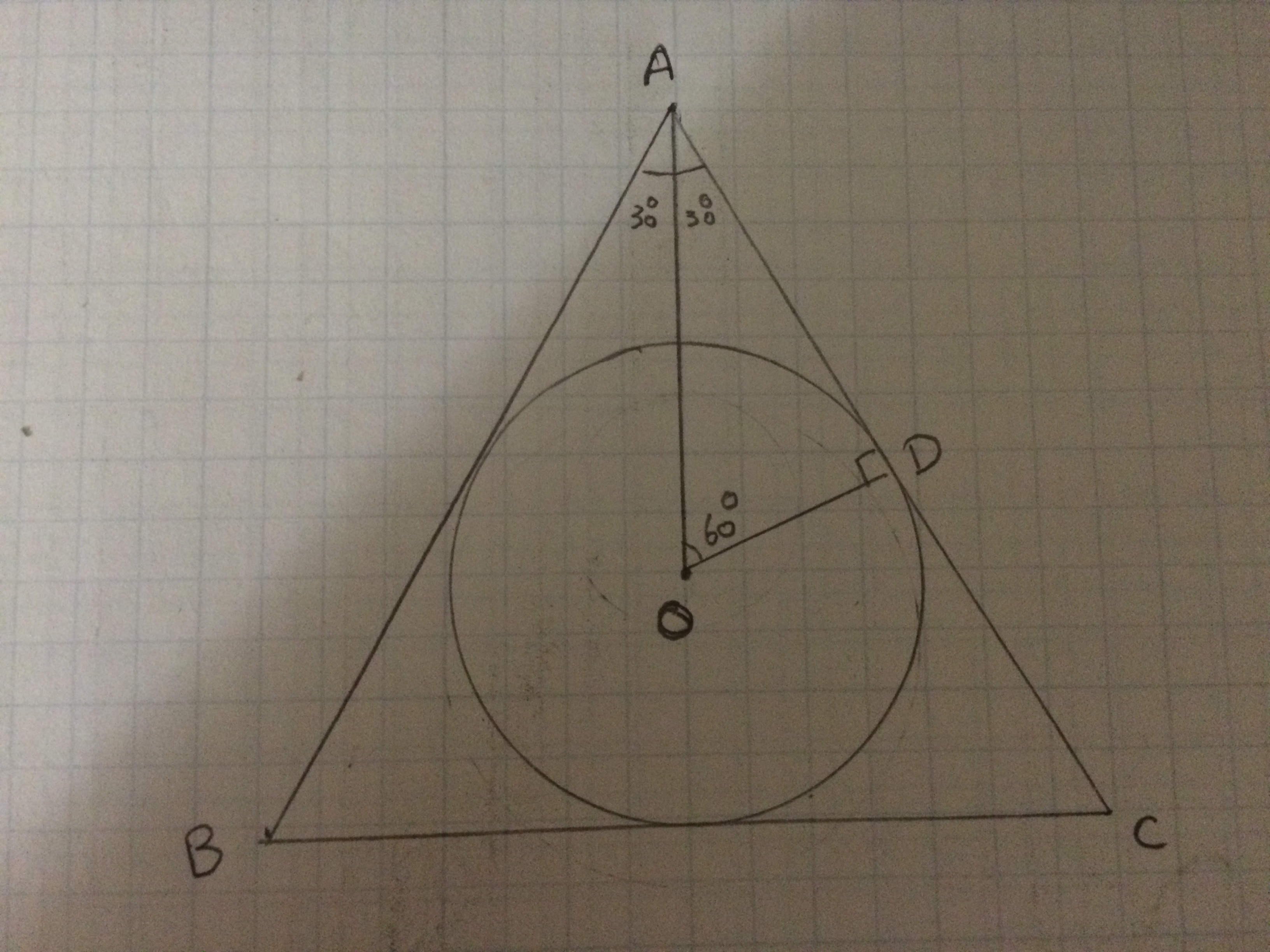
In the above image equilateral triangle ABC is circumscribed about a circle with radius
Triangle OAD is 30-60-90 triangle, the sides have a ratio of:

