An isosceles triangle has sides A, B, and C, such that sides A and B have the same length. Side C has a length of #24 # and the triangle has an area of #48 #. What are the lengths of sides A and B?
1 Answer
Explanation:
Just to clear up what the last contributor had to say, I will write a second answer.
Here is a diagram of the given problem.
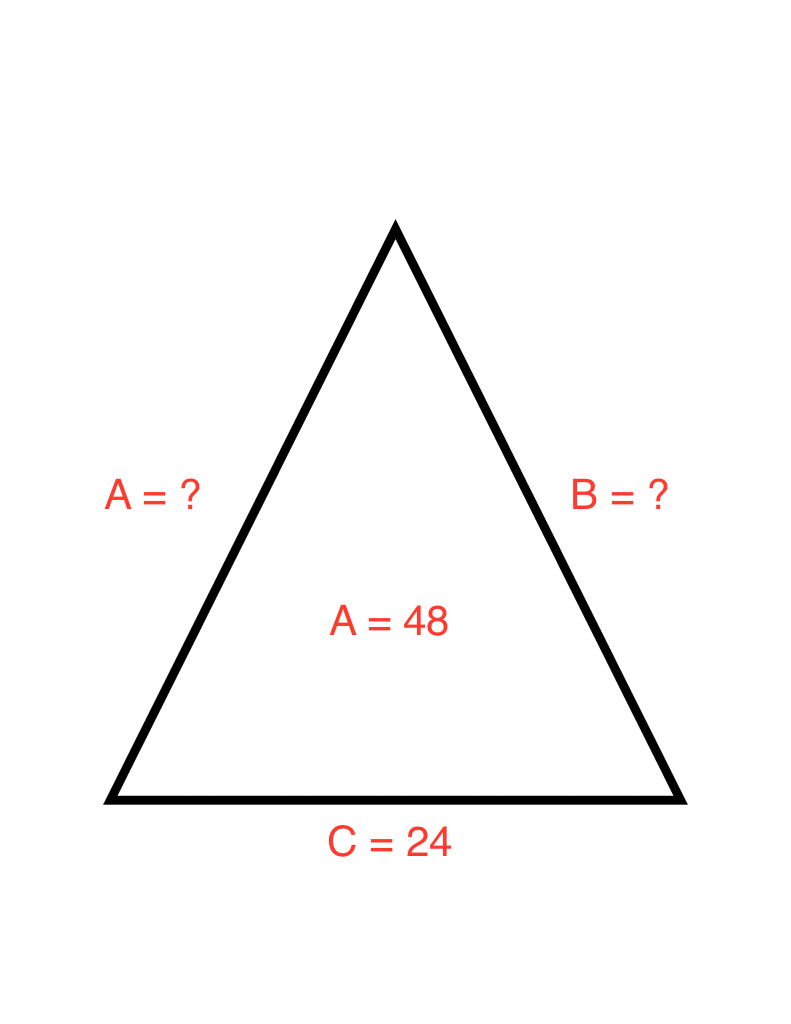
You must understand for this problem is that the formula for area of a triangle is
Here's an updated diagram with the height included.
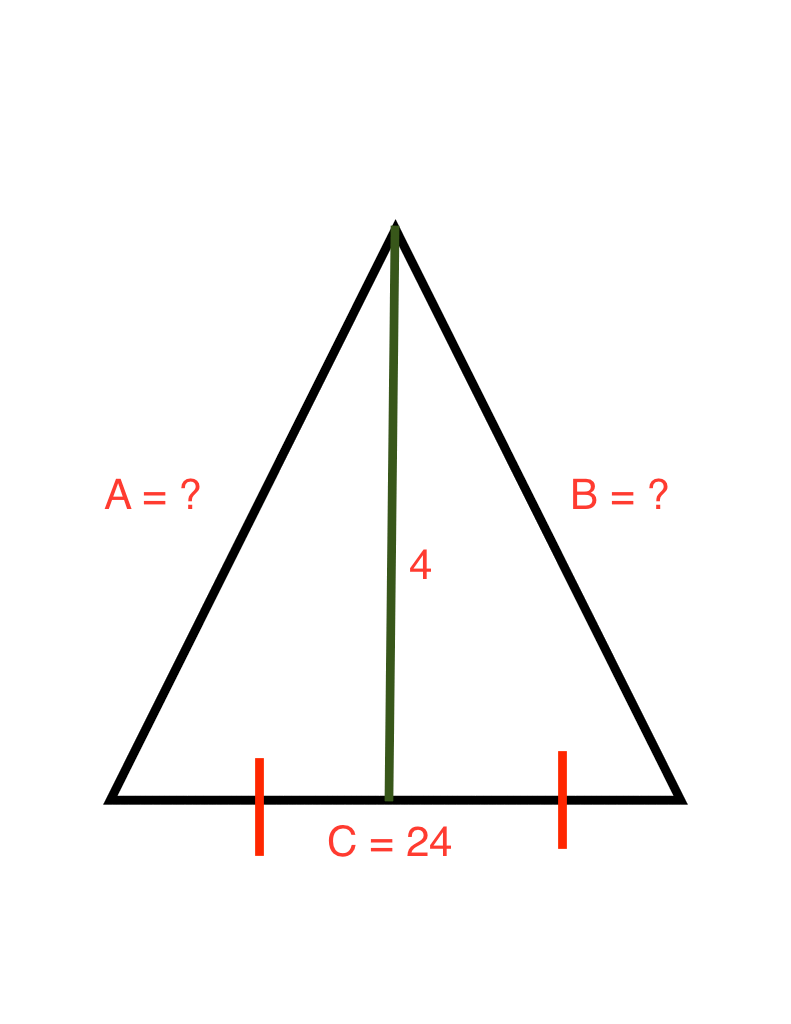
As you can see, I've added the two red bars to signify that the base is cut into two congruent lengths by the height, since we're dealing with an isosceles triangle.
Since the entire base measures
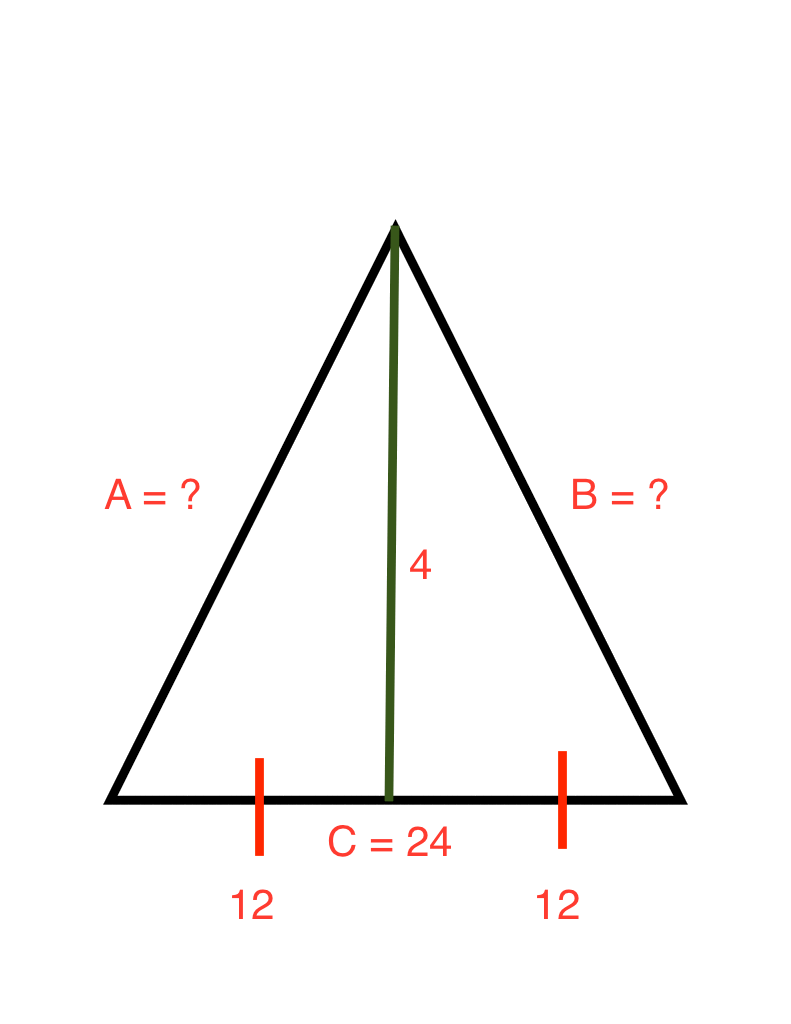
Using pythagorean theorem, we can state:

