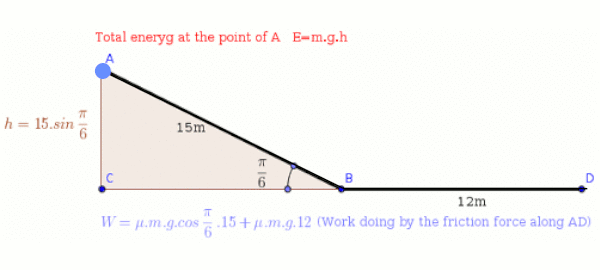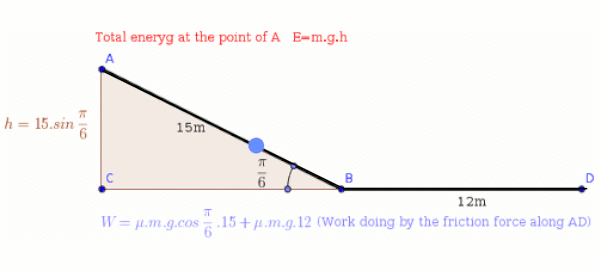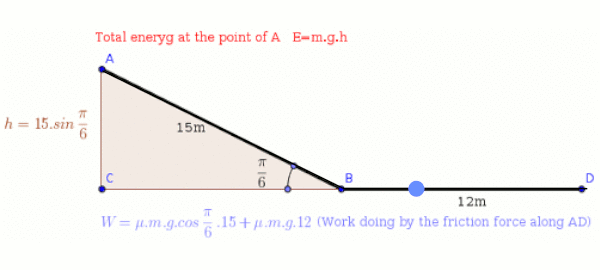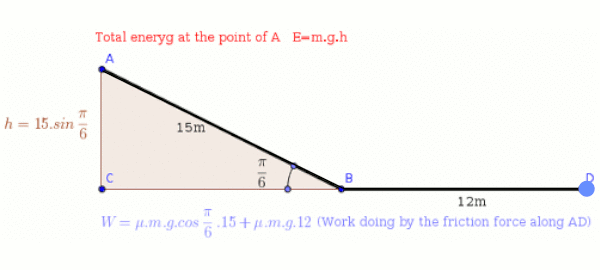
An object, previously at rest, slides #15 m# down a ramp, with an incline of #pi/3 #, and then slides horizontally on the floor for another #12 m#. If the ramp and floor are made of the same material, what is the material's kinetic friction coefficient?
1 Answer
Mar 13, 2016
Explanation: