Question

An object, previously at rest, slides `9 m` down a ramp, with an incline of `(pi)/3`, and then slides horizontally on the floor for another `19 m`. If the ramp and floor are made of the same material, what is the material's kinetic friction coefficient?

Answer 1

`mu_k=0.33`

Explanation:

We are given the angle of incline, displacement of the object down the ramp, and displacement of the object between the bottom of the ramp and its stopping point. We can find the coefficient of kinetic friction using the work-energy theorem.

The first step is to draw a force diagram.

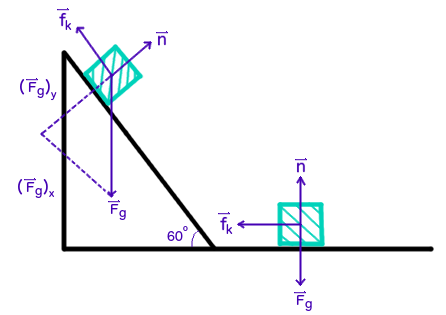
Where `f_k` represents the force of kinetic friction, `n` represents the normal force, and `F_g` represents the force of gravity (both `x`- and `y`-components).

Work-Energy Theorem:

When the object is at rest at the top of the ramp, it possesses only gravitational potential energy, given by `U_g=mgh`. If this were a friction-free system, we would expect all of that potential energy to be converted into kinetic energy as the object slides down the ramp and onto the floor, moving off in that direction forever at at a constant speed (provided there are no other outside forces acting upon it). Because this isn't a friction-free system, we will not see conservation of mechanical energy. The reason the object eventually comes to a stop on the floor is due to friction. This is where energy is lost to as the object slides down the ramp and across the floor.

Work is defined as the mechanical transfer of energy. When the object comes to a stop on the floor, it no longer has either gravitational potential or kinetic energy, but by the Law of Conservation of Energy, we know that the energy had to go somewhere. In this case, if we treat friction as the only outside force energy can be lost to, that means that all of the potential energy stored in the object at the top of the ramp is accounted for in the work done by friction. In other words, the energy lost is equal to the work done by friction. This means that `U_g=W_f`.

Force of kinetic friction: `f_k=mu_kn`

Work done by a constant force: `W=F(Δr)cos(theta)`

Note: In the work equation, `theta` is the angle between the force and displacement vectors. In this case, that angle is `0`. Because `cos(0)=1`, I will omit this part of the calculation below to avoid confusion where `cos(theta)` might come up in other equations.

Note: I will use Δr for the ramp and Δs for the floor to avoid confusion.

The potential energy stored in the object at the top of the ramp is equal to the total work done by friction. This includes both that done on the ramp and the floor (the point where all of the potential energy has been converted is when the object comes to a stop on the floor).

`U_g=W_(Framp)+W_(Ffloor)`

Looking at our force diagram above, we can generate sum of forces statements for when the object is on the ramp and the floor.

Ramp:

`sumF_x=F_(gx)-f_k=ma_x`

`sumF_y=n-F_(gy)=ma_y=0`

(No acceleration in the `y`-direction)

Therefore, `n=F_(gy)`. From our diagram, we can see that `F_(gy)=mgcos(theta)`, and so our equation for kinetic friction on the ramp becomes `f_k=mu_kmgcos(theta)`.

Floor:

`sumF_x=-f_k=ma_x`

`sumF_y=n-F_g=ma_y=0`

Therefore, `n=mg`, and so our equation for kinetic friction on the floor becomes `f_k=mu_kmg`.

For our potential energy, we will need to find `h`. This is the height of the ramp. We can do this using basic trigonometry, where `h=rsin(theta)`.

We now have:

`mgrsin(theta)=(mu_kmgcos(theta))(Δr)+(mu_kmg)(Δs)`

Both the mass, `m`, and `g` are present in each term on both sides and therefore cancel, giving:

`rsin(theta)=(mu_kcos(theta))(Δr)+(mu_k)(Δs)`

We can rearrange to solve for `mu_k`:

`rsin(theta)=mu_k[cos(theta))(Δr)+(Δs)]`

`(rsin(theta))/(cos(theta)(Δr)+(Δs))=mu_k`

Using our known values:

`mu_k=(9sin(pi/3))/(cos(pi/3)(9)+19)`

`mu_k=0.33`

Hope that helps!