An object with a mass of #1 kg# is pushed along a linear path with a kinetic friction coefficient of #u_k(x)= e^x-x+3 #. How much work would it take to move the object over #x in [1, 2], where x is in meters?

Question

1243 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-04-17T12:02:49

The work done is #=65.7J#

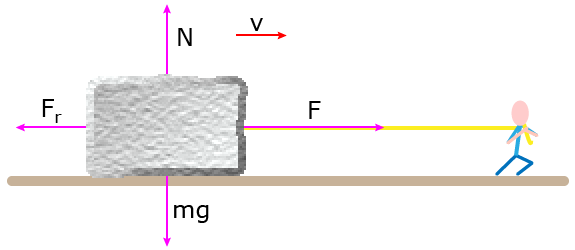
enter image source here

We need

#inte^xxdx=e^x#

The frictional force is

#F=F_r=mu_k*N#

The normal force is #N=mg#

So,

#F_r=mu_k*mg#

#m=1kg#

But,

#mu_k(x)=e^x-x+3#

The work done is

#W=F_r*d=int_0^(pi/12)mu_kmgdx#

#=gint_1^2(e^x-x+3)dx#

#=g[e^x-x^2/2+3x]_1^2#

#=g((e^2-2+6)-(e-1/2+3))#

#=g*(e^2-e+3/2)#

#=6.17g#

#=65.7J#