Question

An object with a mass of `10 kg` is on a plane with an incline of `- pi/4`. If it takes `12 N` to start pushing the object down the plane and `4 N` to keep pushing it, what are the coefficients of static and kinetic friction?

Answer 1

The static coefficient is 1.17; the kinetic coefficient is 1.06.

Explanation:

The object on an incline has one component of the force of gravity pulling it down the slope, usually referred to as `F_(||)`. As the diagram below shows, it is equal to `mgsintheta`

![http://thecraftycanvas.com/library/online-learning-tools/physics-homework-helpers/incline-force-calculator-problem-solver/]!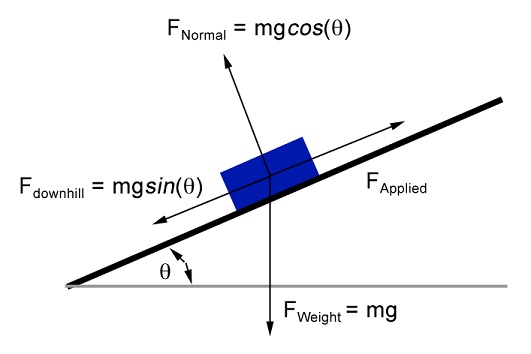

In this problem, the applied force also acts down the incline, and only friction acts up the ramp to oppose these two forces.

The force of friction is given by `F_f = muF_N = mumgcostheta`

Therefore the free body equation is

`F_"net" = mumgcostheta - mgsintheta - F_"applied"`

Since there is no acceleration, `F_"net"=0` and the equation becomes

`mumgcostheta - mgsintheta - F_"applied"=0`

Inserting what we know, I will find `mu_s` first:

`mu_s(10)(9.8)cos( (pi)/4) - (10)(9.8)sin ((pi)/4) - 12 = 0`

Since `cos(pi/4) = sin(pi/4) = .707`

`mu_s(69.3)-(69.3)-12=0`

`mu_s=81.3-:69.3 = 1.17`

The calculation of `mu_k` is similar, using 4N in place of the 12 N applied force:

`mu_k(10)(9.8)cos( (pi)/4) - (10)(9.8)sin ((pi)/4) - 4 = 0`

`mu_k(69.3)-(69.3)-4=0`

`mu_k=73.3-:69.3 = 1.06`