Question

An object with a mass of `10 kg` is on a plane with an incline of `- pi/4`. If it takes `12 N` to start pushing the object down the plane and `7 N` to keep pushing it, what are the coefficients of static and kinetic friction?

Answer 1

`mu_s = 0.173`
`mu_k= 0.101`

Explanation:

`pi/4` is `180/4 deg = 45 degrees`

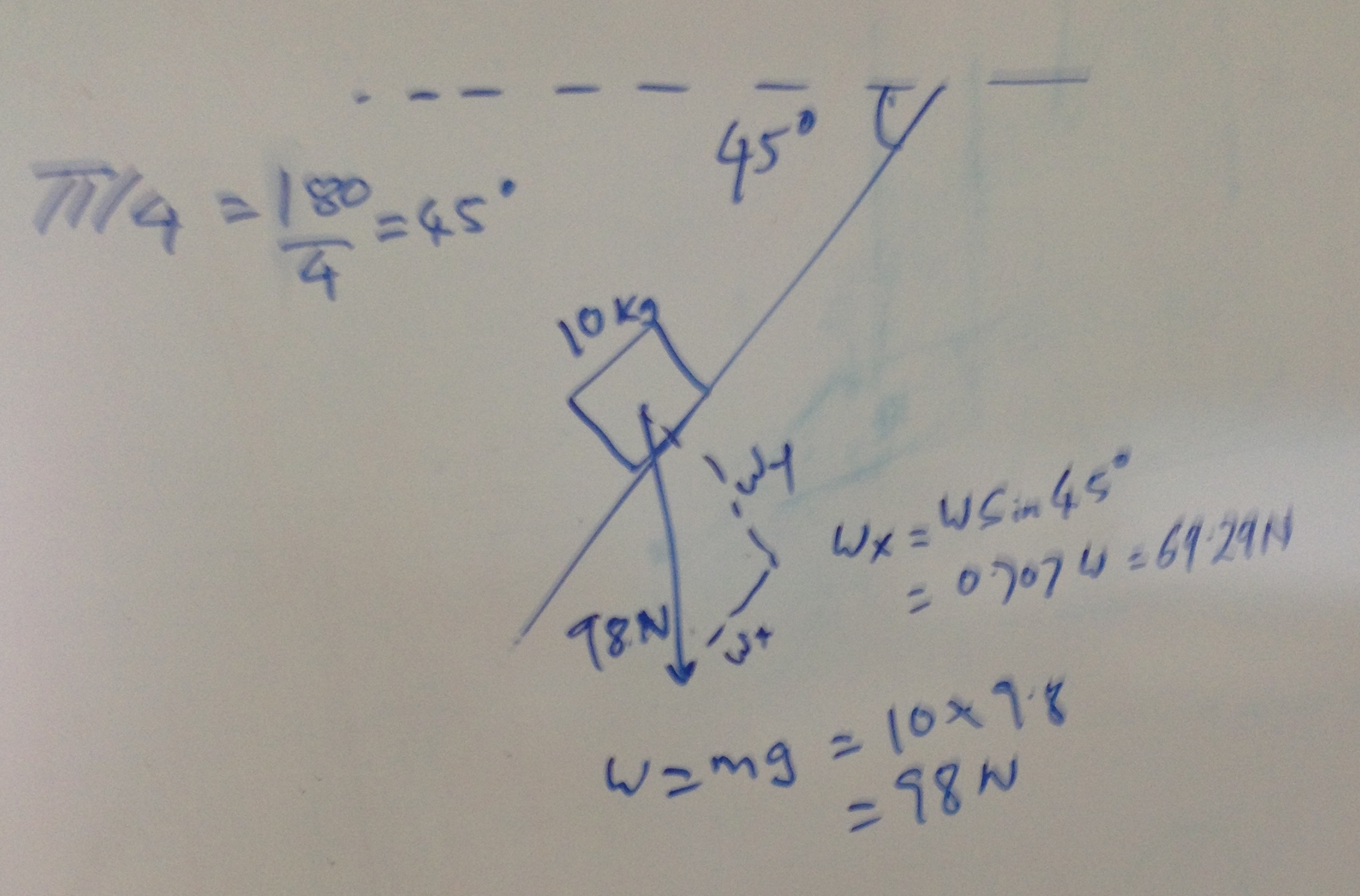
The mass of 10Kg on the incliine resolves to a 98N force vertically.
The component along the plane will be :

`98N * sin45 = 98 * .707 = 69.29N`

Let the static friction be `mu_s`

Static Friction force =`mu_s* 98 * cos 45 = 12`

`mu_s = 12/(98*0.707) = 0.173`

Let kinetic friction be `mu_k`

Kinetic Friction force =`mu_k* 98 * cos 45 = 7`

`mu_k= 7/(98*0.707) = 0.101`