An object with a mass of 10 kg10kg is on a plane with an incline of - pi/4 −π4. If it takes 12 N12N to start pushing the object down the plane and 8 N8N to keep pushing it, what are the coefficients of static and kinetic friction?
1 Answer
Explanation:
The minimum force to start pushing will help to overcome the static friction, so we can calculate the static friction from there.
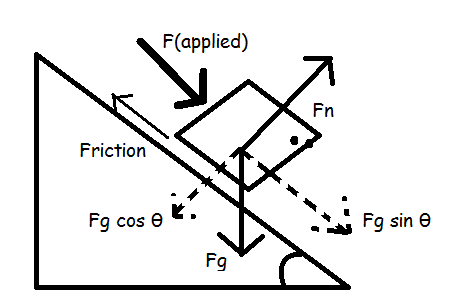 Self created image, ( using MS paint )
Self created image, ( using MS paint )
The Gravitational force acting on the block :
Taking components along the incline and perpendicular to the incline,
and,
Since there is no motion perpendicular to the incline, the net force in that direction will be zero.
Static friction,
According to the question, the value of static friction force happens to be 12N.
Now the kinetic friction will be applicable when the body starts to move.
Kinetic friction,
According to the question, the value of static friction force happens to be 8N.

