An object with a mass of #12 kg# is on a plane with an incline of # -(3 pi)/8 #. If it takes #25 N# to start pushing the object down the plane and #15 N# to keep pushing it, what are the coefficients of static and kinetic friction?

Question

1435 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-05-02T20:59:16

#mu_s = 2.97# and #mu_k = 2.75 #

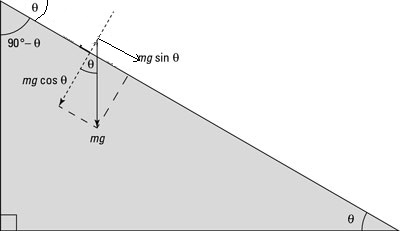
enter image source here

Here, #theta = (3pi)/8#

As we can observe, for both the cases (static and kinetic), the force applied is given as:

#F_(s,k) = mu_(s,k)mgcostheta-mgsintheta#

so, putting #m=12kg#, #theta = (3pi)/8#, and #g=9.8 ms^-2#

#F_(s,k) = 45mu_(s,k)-108.65# (#F# is expressed in Newtons)

#F_s = 25# gives:

#mu_s = 2.97#

and, #F_k = 15# gives:

#mu_k = 2.75 #