An object with a mass of #12 kg# is on a surface with a kinetic friction coefficient of # 1 #. How much force is necessary to accelerate the object horizontally at # 14 m/s^2#?
1 Answer
Explanation:
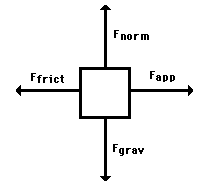
For this problem it is important to note that there are two forces acting on the object in the
Start by listing out the given and required values.
#m=12kgcolor(white)(i)color(teal),color(white)(i)mu_k=1color(white)(i)color(teal),color(white)(i)a=14m/s^2color(white)(i)color(teal),color(white)(i)F_"app"=?#
A free-body diagram can represent the situation as:
In this case, set the positive directions to be forward and down.
Using
#F_("net",y)=ma_y#
#F_N+Fg=ma_y#
Since the object does not accelerate vertically, the acceleration in the
#F_N+Fg=m(0m/s^2)#
#F_N+Fg=0N#
#F_N=-Fg#
#color(blue)(|bar(ul(color(white)(a/a)color(black)(F_N=-mg)color(white)(a/a)|)))#
After adding the forces in the
#F_("net",x)=ma_x#
#F_"app"+F_(f,k)=ma_x#
#F_"app"=ma_x-F_(f,k)#
#F_"app"=ma_x-mu_kF_N#
#F_"app"=ma_x-mu_k(color(blue)(-mg))#
#F_"app"=ma_x+mu_kmg#
Substitute your known values.
#F_"app"=(12kg)(14m/s^2)+(1)(12kg)(9.81m/s^2)#
#F_"app"=285.72N#
#F_"app"~~color(green)(|bar(ul(color(white)(a/a)290Ncolor(white)(a/a)|)))#