Question

An object with a mass of `15 kg` is on a ramp at an incline of `pi/8`. If the object is being pushed up the ramp with a force of `7 N`, what is the minimum coefficient of static friction needed for the object to remain put?

Answer 1

`mu_s<=0.363`

Explanation:

We are given the following information:

• `|->m=15"kg"`
• `|->theta=pi/8`
• `|->F_a=7"N"`

Two important points about static friction...

• Recall that it is the force of maximum static friction which is proportional to the magnitude of the normal force, `n`, and that `f_s<=f_(s"max")`

• The direction of the force of static friction acting on an object is opposite the direction that the object would move if the force of friction was not present

We can calculate the coefficient of friction at the maximum force of static friction, where our forces are in equilibrium. Keep in mind that an object remains at rest as long as `f_s < f_(s"max")` and that the object begins to slip when `f_s=f_(s"max")`.

The force of friction in question then should be less than `f_(s"max")`. Therefore, we cannot calculate the exact coefficient you are looking for; we can only give the coefficient that it must be less than (that of maximum static friction).

Conclusion: `vecf_s<=mu_sn` (direction as necessary to prevent motion).

A diagram of the situation:

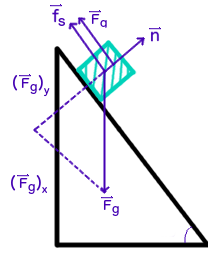
Let's define up the incline as positive.

Summing the parallel (x) and perpendicular (y) components of our forces, we have:

`(1)" "color(darkblue)(sumF_x=f_s+F_a-(F_G)_x=cancel(ma_x)=0)`

`(2)" "color(darkblue)(sumF_y=n-(F_G)_y=cancel(ma_y)=0)`

We also know that:

`(3)" "color(darkblue)(f_(s"max")=mu_sn)`

`(4)" "color(darkblue)(F_G=mg)`

Substituting equations `(2)` and `(3)` into equation `(1)`, we have:

`(5)" "color(darkblue)(mu_s(F_G)_y+F_a-(F_G)_x=0)`

We can rearrange equation `(5)` to solve for the coefficient of static friction.

`=>(6)" "color(darkblue)(mu_s=((F_G)_x-F_a)/(F_G)_y)`

We can find the components of the force of gravity using trigonometry.

`sin(theta)=(F_G)_x/F_G`

`=>(F_G)_x=F_Gsin(theta)`

Similarly, `(F_G)_y=F_Gcos(theta)`

By equation `(4)`, we have:

• `(F_G)_x=mgsin(theta)`

• `(F_G)_y=mgcos(theta)`

We can substitute these equations into equation `(6)`:

`color(crimson)(mu_(s"max")=(mgsin(theta)-F_a)/(mgcos(theta))`

Now we can substitute in our known values:

`=>mu_(s"max")=((15"kg")(9.81"m"//"s"^2)sin(pi/8)-7"N")/((15"kg")(9.81"m"//"s"^2)cos(pi/8))`

`=0.363`

`:.` The coefficient of static friction is `<=0.363`.